マクロ経済学第14回のテーマは「IS-LMモデル分析③」です。以下、全体の目次です。
目次：「IS-LMモデル分析③―公債の市中消化・中央銀行引受」
2．財源①：租税（増税）
3．財源②：公債の市中消化
4．財源③：公債の中央銀行引受
5．リカード＝バローの等価定理（中立命題）
前回、「IS-LMモデル分析①」「IS-LMモデル分析②」では、IS-LMモデルを使い財政政策と金融政策の効果についてまとめてきました。基本的な事項は、以下の記事をご参考ください。
今回は、財政政策を実施する場合、必ずその財源はどこから支出されるの？というテーマがあります。
財源の確保には2パターンあり、それは租税（増税）と公債の発行です。
本記事では、IS-LMモデル分析を使い、財源の観点から財政政策の効果について深掘りしていきたいと思います。
【マクロ経済学】IS-LMモデル分析③【公債の市中消化・中央銀行引受】
財源の観点から、財政政策の効果を理解する。
【IS-LMモデル分析】財政政策の財源―租税（増税）・公債
拡張的な財政政策（政府支出の増加）を行う場合、その財源をどこに求めるのかという議題があります。
この財源を賄う方法として、3パターンあります。
1．租税（増税）
2．公債の市中消化
3．公債の中央銀行引受（原則禁止）
財源を租税（増税）で賄うパターンと政府が公債（国債）を発行して賄うパターンです。また公債の場合、どこがその公債を引き受けるかにより、財政政策の効果が変わります。
一つは、発行した公債を民間銀行が引き受ける市中消化のパターン、もう一つは中央銀行が引き受けるパターンです。
以下、グラフとともに、３つの財政政策の効果について確認していきます。
【IS-LMモデル分析①】財政政策の効果（租税―増税）
まずは、モデルとしてシンプルな閉鎖経済の需給均衡式を考えます。
需給均衡式：$\small Y= C+I+G$
消費関数：$\small C= c_0+c_1(Y-T)$
投資・政府支出・租税：$\small I, G, T$＝一定（かつ定額税）
⇔$\small Y= c_0+c_1(Y-T)+I+G$
⇒$\small (1-c_1)Y= c_0-c_1T+I+G$
⇒$\small Y=\frac{1}{(1-c_1)}[c_0-c_1T+I+G]$
このとき、政府支出の財源を租税で賄うため、等式としては$\small ⊿G=⊿T$となります。
これは均衡予算を意味しているため、$\small T=G$より
$\small ⊿Y=\displaystyle \frac{1-c_1}{1-c_1}⊿G$
$\small ⊿Y=⊿G$
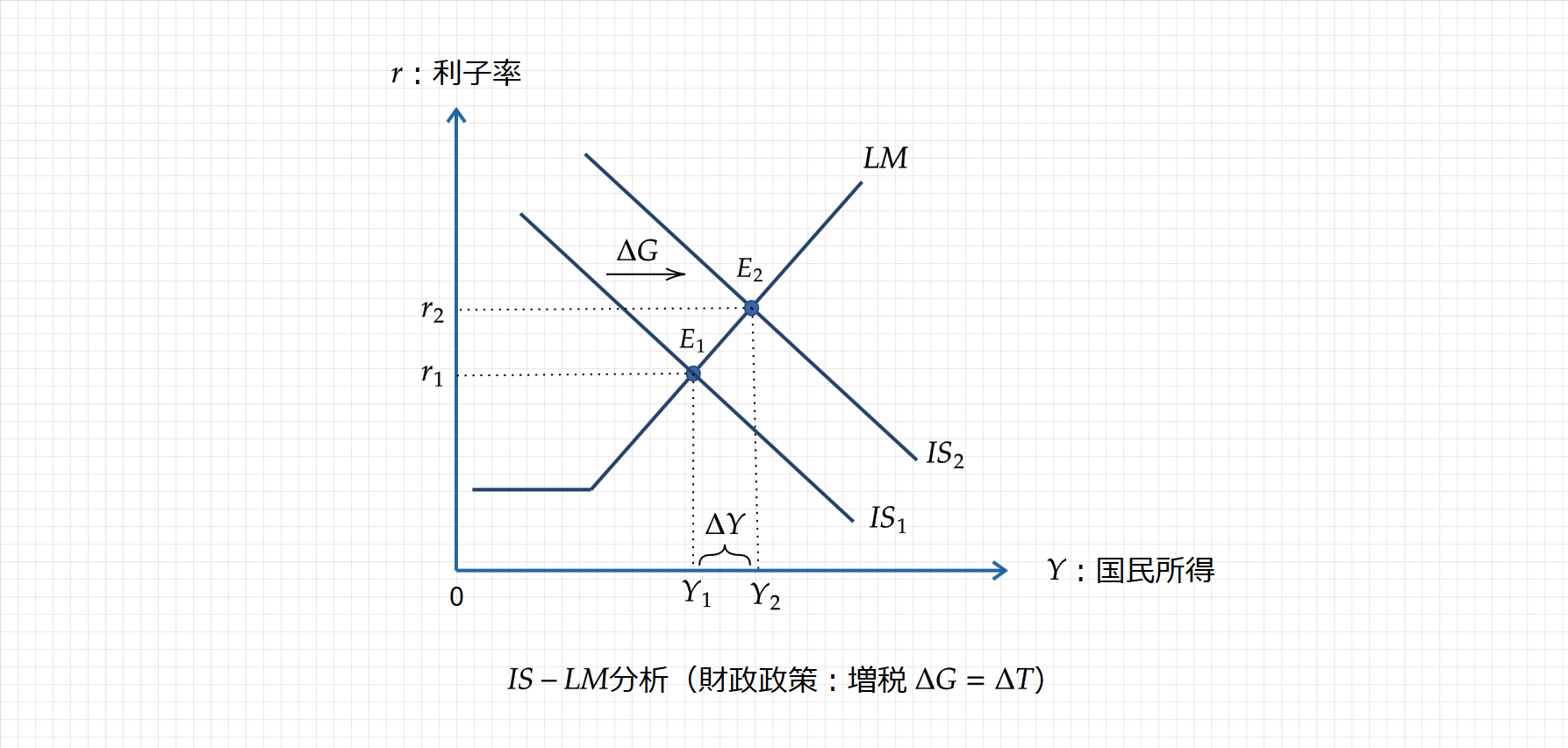
となります。つまり、政府支出を増加させた分だけ、国民所得が増加することになります（下図）
本来なら、乗数効果が働くところですが、均衡予算のため、政府支出乗数は１となり、政府支出を増やした分だけ、国民所得が増加する形となります。
以上が、財源を租税（増税）で賄った場合のパターンです。
【IS-LMモデル分析②】財政政策の効果（公債の市中消化）
次に、公債の市中消化の場合はどうでしょうか。財源を公債に求めるため、増税せずに財源調達することが可能となります。
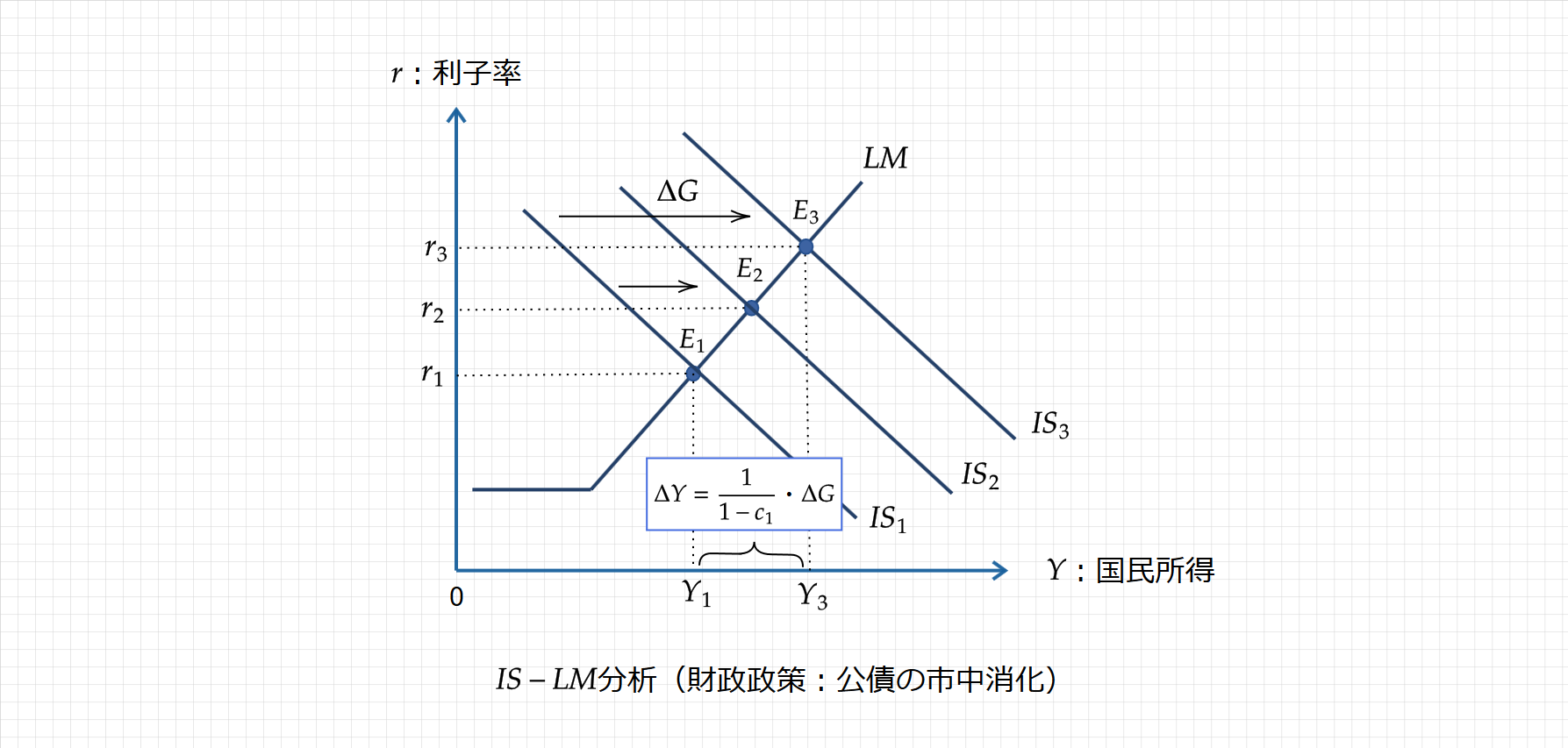
したがって、政府支出乗数は、$\small \displaystyle \frac{⊿Y}{⊿G}=\frac{1}{1-c_1}$となります。
租税（増税）と比較すると、国民所得は政府支出に$\small \displaystyle \frac{1}{1-c_1}$を乗じた分だけ増えています（租税による消費の減退がないため）。
⇒IS曲線は増税の時よりも、右にシフトする。
これが、公債の市中消化により財源を賄った場合の財政政策の効果となります。
【IS-LMモデル分析③】財政政策の効果（公債の中央銀行引受）
最後は、公債の中央銀行引受の場合です。ポイントは次の2つです。
1．中央銀行がその公債（国債）を購入するため、増税せずに財源調達可能
2．中央銀行が公債を購入するため、ハイパワード・マネーが増大する
中央銀行が公債を引き受けることにより、マネーストックが増加し、金融緩和政策の効果も同時に発生する。
（※現在は過度なインフレが発生する可能性があるため、財政法上は原則禁止されている）
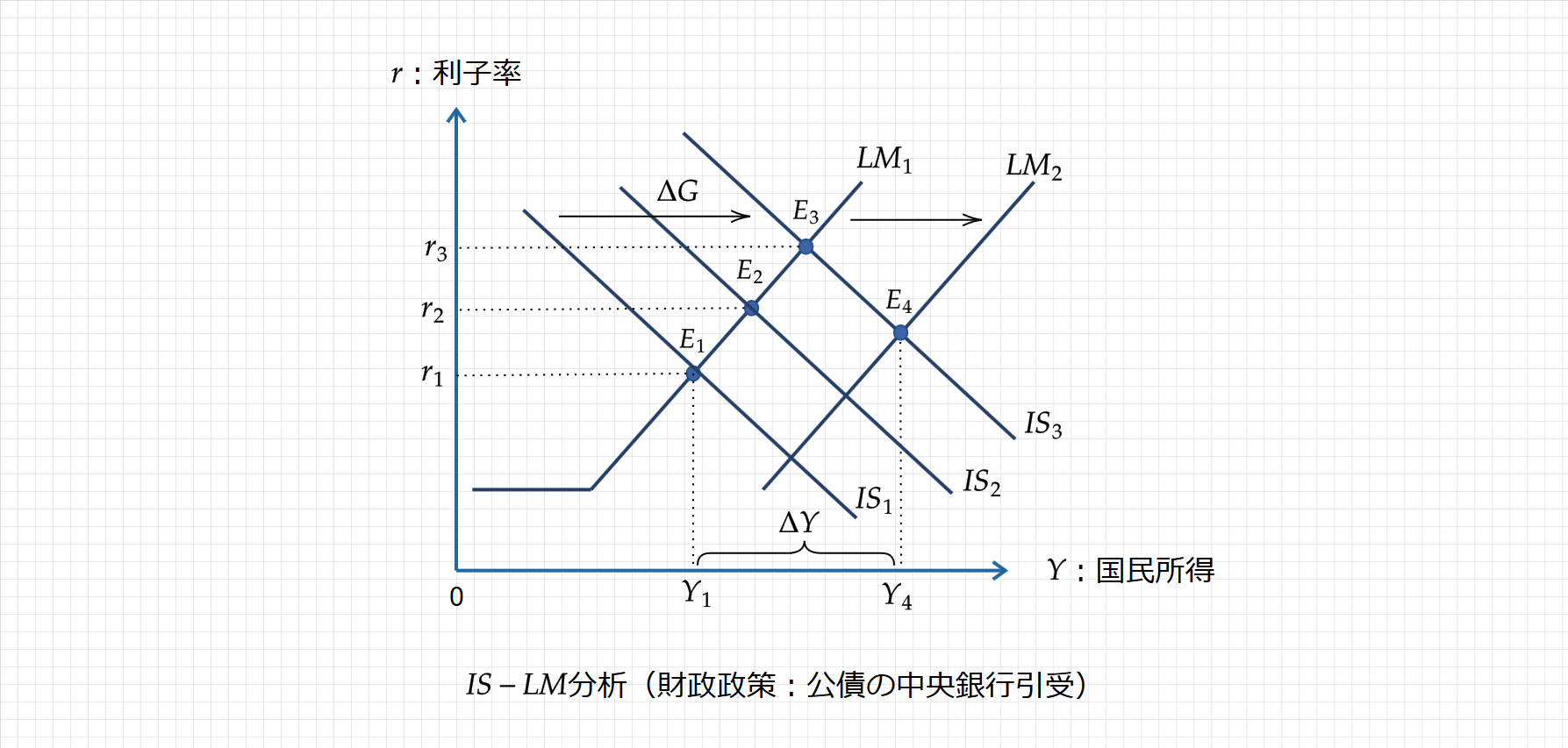
理論上、中央銀行による公債引受は、拡張的な財政政策と金融緩和政策の効果をもたらします（下図）。
実質的な金融緩和効果により、IS曲線だけでなくLM曲線も右にシフトします。
したがって、国民所得は$\small Y_1$から$\small Y_4$まで増加します。
これが、公債の中央銀行引受により財源を賄った場合の財政政策の効果である。
ここからさらに議論を掘り下げて、公債負担論について「リカード＝バローの等価定理」をまとめていきます。
【IS-LMモデル分析】公債負担とリカード＝バローの等価定理（中立命題）
リカードの等価定理とバローの中立命題を理解する。
リカードの等価定理（中立命題）
ここでの論点は「公債を誰が負担するのか？」ということです。
D.リカード
リカードの主張
結局、政府支出の財源を公債を発行して確保したとしても、将来的には課税により徴収しなければならないから、公債の発行と増税による政策効果は等しくなる。
まとめると、、、
公債の発行は、将来の課税を意味するため、現役世代は将来における公債償還のための増税に備え、消費を減少させて貯蓄を増加させます。つまり、これは均衡予算の考え方から見れば、増税の政策効果と同じとなるため、政府支出乗数もまた$\small \frac{ΔY}{ΔG}=1$となる。
（※ただし、公債の発行と償還は、現役世代が生存期間内に行われること。）
これを「リカードの等価定理（中立命題）」といいます。
ポイントは、「公債の発行と償還は、現役世代が生存期間内に行われる」
⇒現役世代内で負担すると主張！
では、バローの中立命題は一体何でしょうか？？
公債負担論②：バローの中立命題
これに対して、数多くの経済学者が「公債の負担は将来世代に転嫁される」と反論しました。
ざっくりまとめると、、、
将来世代に転嫁される（新古典派）：ブキャナンやモディリアーニ
将来世代に転嫁されない（合理的期待形成学派）：新リカード学派やバローの中立命題
将来世代に転嫁される論派は、公債の発行が利用資金の減少や資本蓄積（民間貯蓄）の減少により、将来の増税や将来所得の減少をもたらす、と主張しました。
一方、リカードやバローは、公債の負担が将来世代に転嫁されないことを主張しています。
ここで登場するのが「バローの中立命題」です。
公債償還が世代を超えて行われる場合でも、現在世代が将来における償還のための増税を予想して貯蓄を増やし、将来世代に遺産を残そうとすれば、世代を超えてリカードの等価定理が成立し、負担は転嫁しない。
（バローはこのように遺産を残す動機を、利他的動機と呼んでいます。）
つまり、遺産により将来世代の負担が相殺される可能性（将来世代に転嫁されない）を示唆しました。バローは、これを数理モデルで表現し、公債の中立性を主張しています（ここでは省略します）。
このような理論的背景から、「リカード＝バローの中立命題」と呼ばれています。
リカード＝バローの等価定理の成立条件と問題点
最後に、リカード＝バローの等価定理の成立条件と問題点についてまとめていきます。
リカードの中立命題は、非常に仮想的な状況を想定していることに留意すべきです。
以下、リカードの中立命題における主要な仮定となります。
1．現在から将来にかけての政府の支出計画はあらかじめ定められており、政府は計画された支出の執行が義務付けられる。
2．政府は、すべての家計に一括税（ランプ・サム税）を課すことができる。
3．政府の国債発行による資金調達は、実質利子率レートで行うことができる。
このような仮定を想定しているため、かなり非現実的であると批判されています。
以上をもとに、リカード＝バローの中立命題の成立条件を要約すると、次のようになります。
①：すべての個人が合理的である＝合理的経済人（合理的期待形成学派）
⇒将来の増税を見越して、行動することができる
②：現在の世代と将来の世代が利他的に結びついている
⇒将来の子孫のことを考えて行動できること：利他的行動
③：家計（個人）の流動制約がない（資金を自由に借り入れすることができる）
④：課税は一括税で行う（すべての家計に対して一律で課税）
すべて成立するには、あまりにも非現実的という感じです。
実証分析でも、やはり新古典派の主張を支持するような結果が報告されています。
以上、公債の市中消化・中央銀行引受・リカード＝バローの等価定理でした。
おわりに：試験ではちょこちょこ出る
大学の定期試験・公務員試験・大学編入・大学院入試でも、ちょこちょこ出題されます。
論点が明確なところや、公債論はホットトピックであり、かつ経済学の議論として一歩踏み込んでいるため、色んなところで見かけます（財政学の論点ですし）。
以上となります。参考になった方は応援もよろしくお願いします！
【参考文献】
齋藤誠他（2016）『マクロ経済学 新版』有斐閣.
大竹文雄（2007）『スタディガイド 入門マクロ経済学(第5版)』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】
コメント