こんにちは、とし(@tyobory)です。
今回からミクロ経済学のトピックは「予算制約線と効用最大化」です。以下、全体の目次です。
目次:「予算制約線と効用最大化(消費者行動)」
- 予算制約線と最適消費計画 ⇦ 今ココ
- 所得の変化と最適消費
- 価格の変化と最適消費
- 代替効果と所得効果
ミクロ経済学第4回のテーマは「予算制約線と最適消費計画」です。
過去記事で「無差別曲線」を取り扱いましたが、私たちはモノを無限に消費できるわけではなく、必ず予算の制約があります。予算制約内で財を買い、消費します。
以下、予算制約線に基づく最適消費について掘り下げていきます。
【ミクロ経済学】予算制約線と最適消費計画【効用最大化条件を理解する】

効用最大化条件を押さえる。
予算制約と最適消費計画のイメージ
予算制約と最適消費計画は、グラフや数式よりも、次のようなイメージの方が理解しやすいです。
| 子どもの頃、お小遣いをもらって好きなお菓子を買った記憶と一緒です。このとき、お小遣いをギリギリまで使い切り、自分の満足度が最大になるようにお菓子選びをした思います。 |
「予算制約と最適消費計画」もこのイメージそのまんまで、「財を組み合わせて、予算を使い切る」、これが本質です。
このイメージを経済学的にグラフや数式で可視化したものが、「予算制約線と最適消費計画」となります。
予算制約線を書けるようになる【グラフと数式で理解】
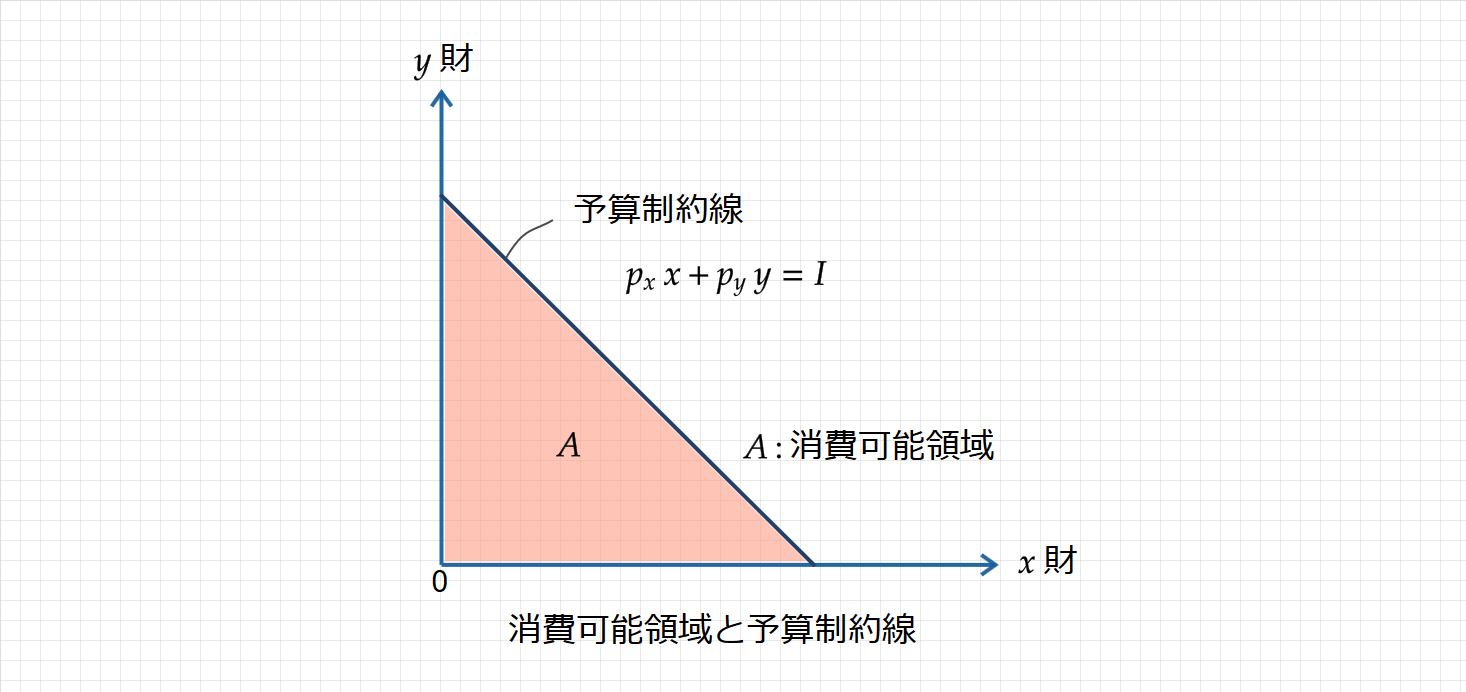
最適消費計画を考えるとき、たいてい2財の消費のみのケースを取り扱い、予算制約線は次のように図示されます。
人々の所得を$\small I$(Income)、$x$ 財の価格を$p_x$、$y$ 財の価格を$p_y$とすると、支出額は${p_x}x+{p_y}y$と表すことができます。所得を使い切るように財を消費するため、所得=支出より、
$\small {p_x}x+{p_y}y=I$ $\\$ $\small y=-\frac{\displaystyle p_x }{\displaystyle p_y}x+\frac{\displaystyle I}{\displaystyle p_y}$
となります。このように$y=…$で直した予算制約線内で、財の組み合わせを考えます。
Aの部分は消費可能領域で、予算制約線より上だと予算オーバーとなり、実現しない財の組み合わせになります。以下、最適消費計画を考えていきます。
予算制約線と最適消費計画【無差別曲線を書き加える】
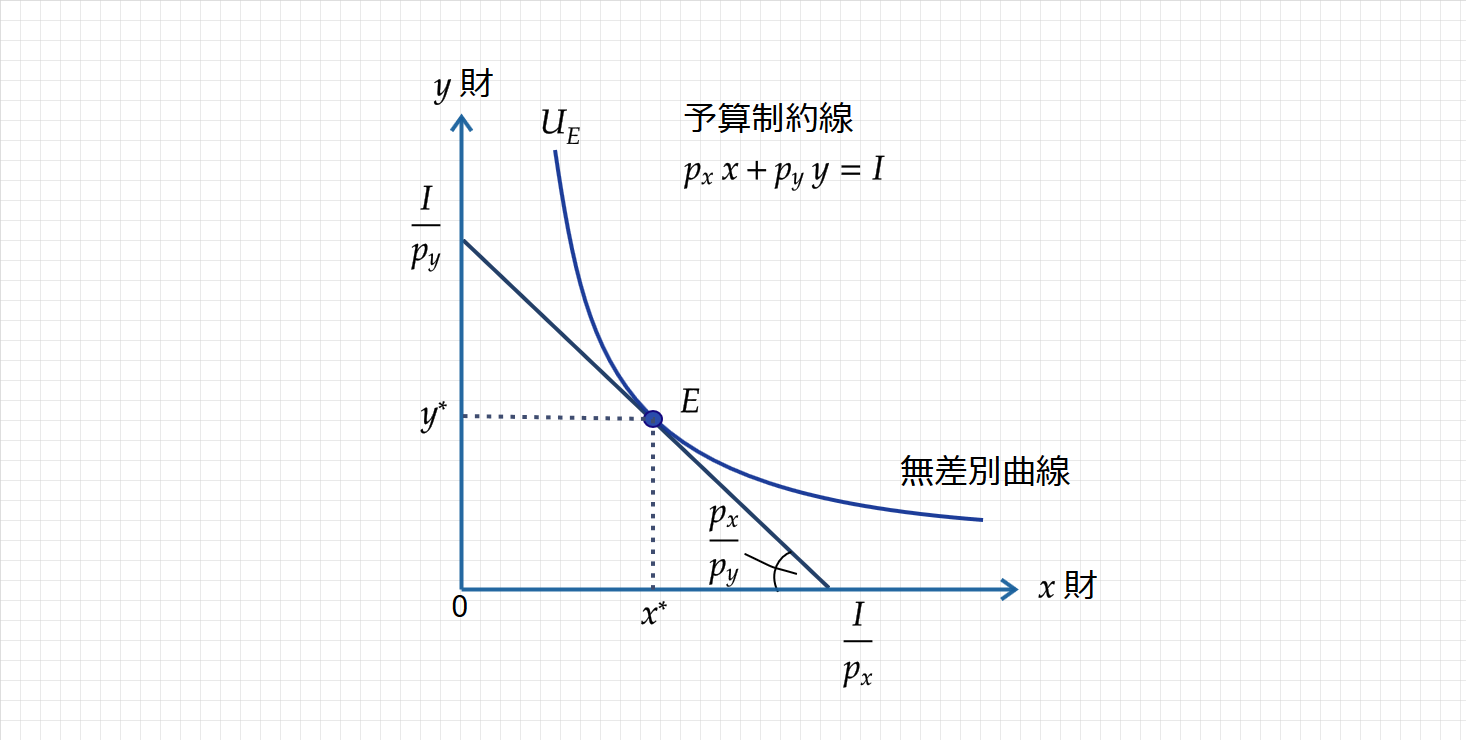
下図は、無差別曲線と予算制約線を書き加えたものになります。
結論から言うと、無差別曲線と予算制約線が接する点である$\small E$点が最適消費点となります。
つまり、$\small E$点の消費量で、効用関数 $\small U$ のもと効用最大化が達成されています。
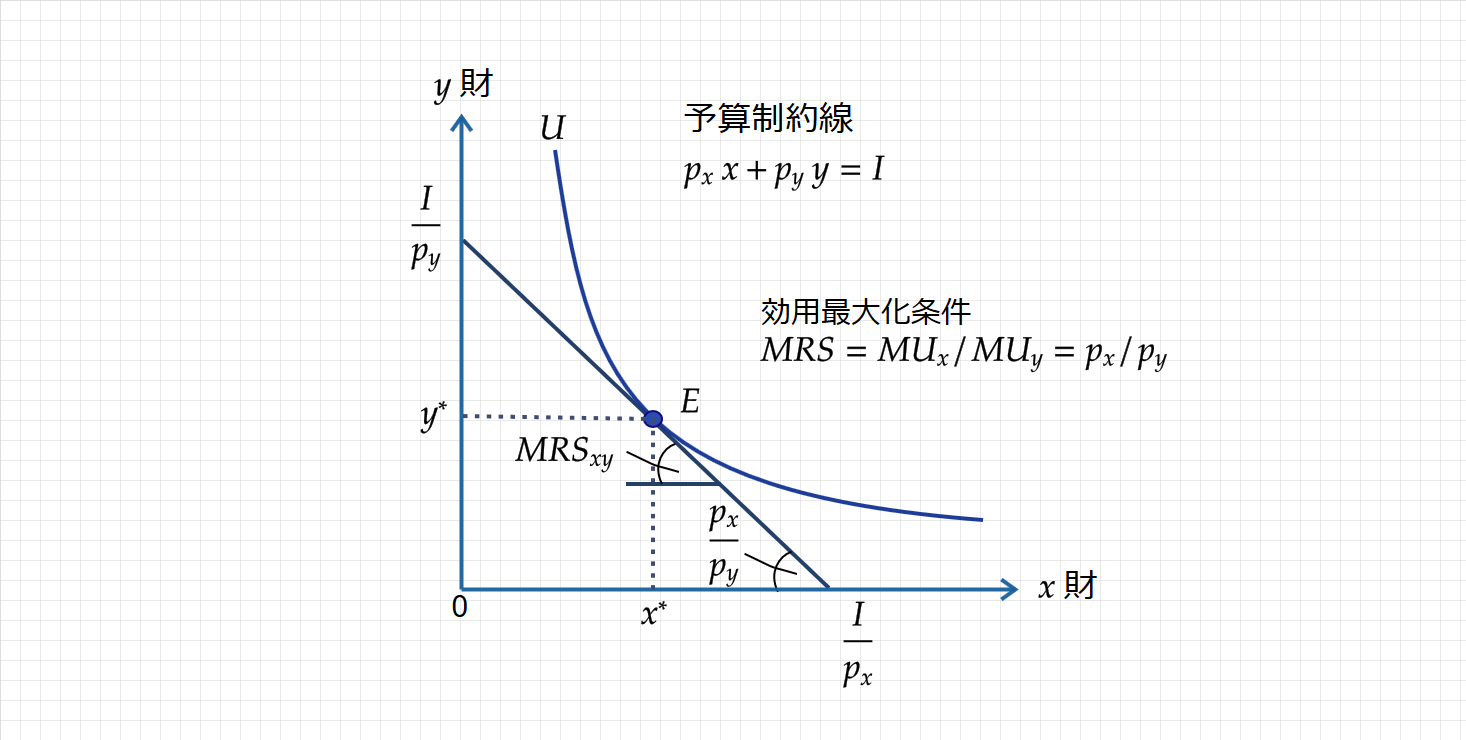
ここで、効用最大化条件をまとめると次のようになります。
$\small 効用最大化条件:MRS=\frac{\displaystyle MU_x}{\displaystyle MU_y}=\frac{\displaystyle p_x}{\displaystyle p_y}$
そうなんです。限界代替率($\small MRS$)の大きさと財の価格比($p_x$/$p_y$)が等しいとき、効用最大化が達成されているのです。上式を書き換えると、さらに理解が深まります。
$\small 加重限界効用均等の法則:\frac{\displaystyle MU_x}{\displaystyle p_x}=\frac{\displaystyle MU_y}{\displaystyle p_y}$
$\frac{1}{p_x}$ は分母が価格のため、「1円当たりの消費量」と解釈できます。
そのため、1円あたり得られる $x$ 財の限界効用=1円あたり得られる $y$ 財の限界効用となります。
つまり、$\small E$点から、最後の1円を$x$ 財と $y$ 財どちらに消費量を振り分けても、得られる効用に変化ない状態で、$\small E$点が最適な消費点として表されます。
予算制約線と最適消費の演習問題
問題
以下のような消費者の効用関数を考える。
$u( x , y )=xy^3$
($x$ :$x$ 財の消費量、$y$ :$y$ 財の消費量)
$x$ 財の価格が $p_x=2$ 、$y$ 財の価格が $p_y=1$ 、所得が $I=8$ のとき、$x$ 財と $y$ 財の最適な消費量を求めなさい。
解答
まず、最適消費計画における効用最大化問題は次のように定式化される。
$\underset{x,\,y}{Max} u( x , y )$ $\\$ $s.t {p_x}x+{p_y}y=I $
つまり、それぞれの値を代入すると、
$Max u( x , y )=xy^3$ $\\$ $s.t 2x+y=8 $
となる。効用最大化条件は、限界代替率($\small MRS$=$\small MU_x/MU_y$) = 予算制約線の傾きの価格比($p_x/p_y$)であるため、$MU_x=y^3$、$MU_y=3xy^2$より、
$MRS=\frac{\displaystyle y^3}{\displaystyle 3xy^2}=\frac{\displaystyle 2}{\displaystyle 1}$ $\\$ $y=6x$
$y=6x$を予算制約式に代入すると、(答)$x^*=1$、$y^*=6$が求められる。
※ポイントは、効用最大化問題を正しく定式化できること、限界代替率(MRS)=価格比を使うことです。
おわりに:効用最大化条件をしっかり理解する
今回は予算制約線と最適消費点についてまとめてきました。
おさらいすると、
1.最適消費点は無差別曲線と予算制約線が接する点
2.効用最大化条件は$\small MRS = MU_x/MU_y$ = 価格比($\small p_x/p_y$)

以上となります。参考になった方は応援もよろしくお願いします!
【参考文献】
尾山・安田(2013)『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏(2014)『ミクロ経済学の力』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】



コメント