こんにちは、とし(@tyobory)です。
ミクロ経済学の「効用関数と無差別曲線」の第2回です。
目次:効用関数と無差別曲線(消費者行動)
第1回の「限界効用」では、財を消費することで得られる効用について学びました。未学習の方は下記記事をご参考ください。
今回のテーマは「無差別曲線」という概念で、2種類の財を同時に消費したときの効用について考えます。
以下、「無差別曲線」について掘り下げていきます。
【ミクロ経済学】無差別曲線とは?【グラフで解説】

無差別曲線を知る。
「無差別曲線(Indifference curve)」を押さえる【一般的な形】
「無差別曲線」は等効用線と呼ばれ、同じ効用が得られる財の組み合わせとして定義されます。
ミクロ経済学の教科書では、グラフで書ける範囲として、2種類の財を同時に消費したときの効用を考えます。以下、無差別曲線のグラフです。
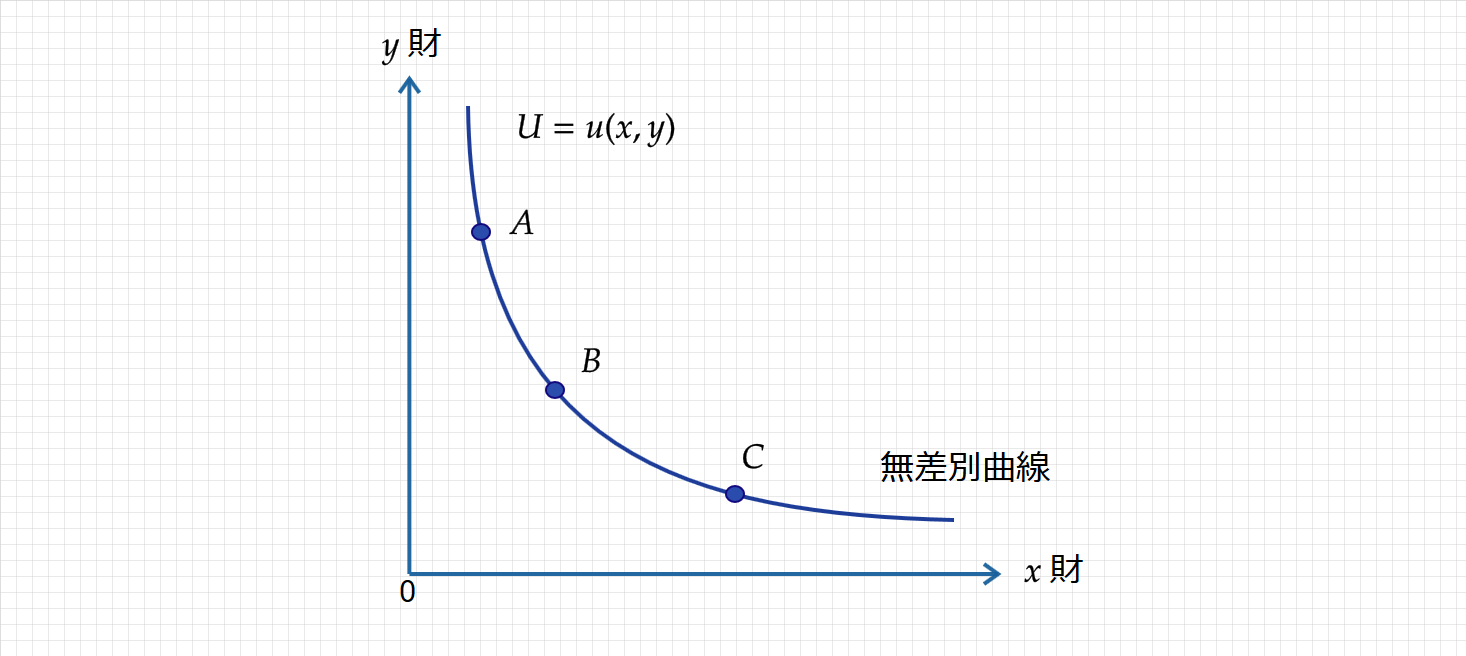
図のように、横軸に $x$ 財、縦軸に $y$ 財の消費量をとったとき、同じ効用水準の財の組み合わせを表す点をつなげたものが無差別曲線である(A,B,Cでは同じ効用水準)。
この一般的な無差別曲線は4つの特徴があります。
①:右下がり
②:右上方に位置するほど効用は高い
③:原点に対して凸状となる
④:異なる曲線は互いに交わらない
それぞれ詳しく見ていきましょう。
性質①:右下がり
無差別曲線の性質として、「右下がり」があります。
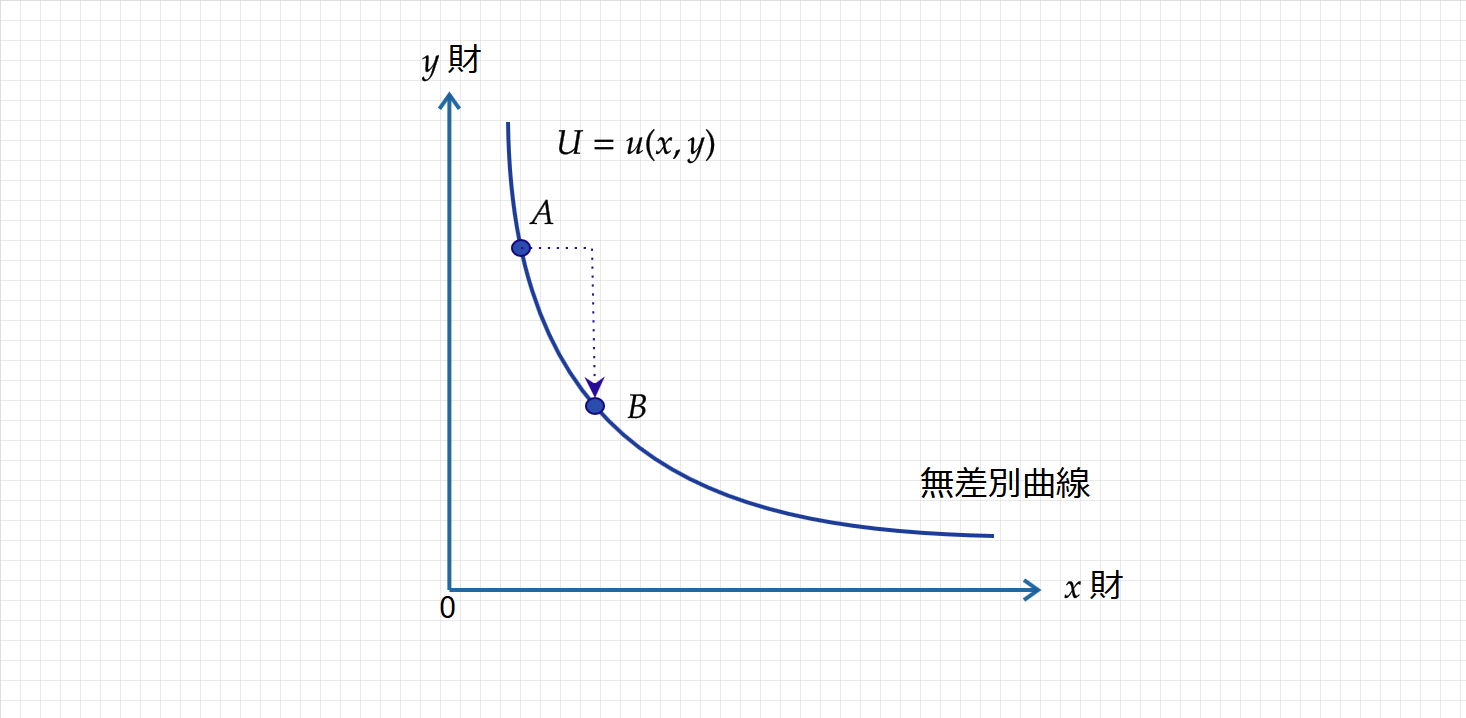
無差別曲線は同じ効用が得られる財の組み合わせのため、点Aから $x$ 財の消費量を増やすならば、もう片方の $y$ 財の消費量を減らさなければなりません。これが「右下がり」の性質です。
性質②:右上方に位置するほど効用は高い
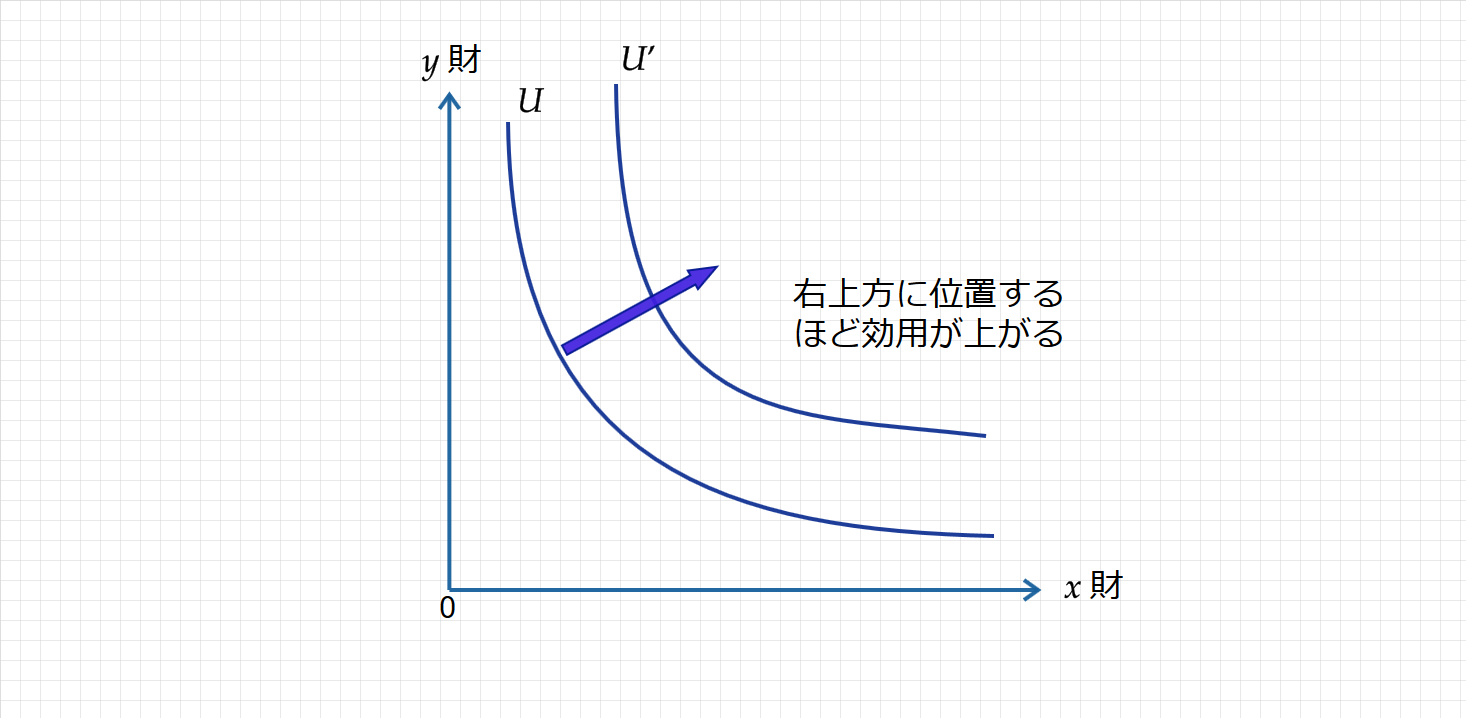
無差別曲線は無数に存在し、右上方に位置するほど効用は高くなります。
ここで、 $x$ 財の消費量が増えて、 $y$ 財の消費量が減らないなら、効用水準が上昇することに対応します。
つまり、たくさん消費すればするほど、効用水準が高くなります(ただし、不飽和を仮定する)。
性質③:原点に対して凸状となる
3つ目に無差別曲線は原点に対して凸状の形をしているということです。
無差別曲線の接線の傾きは $x$ 財と $y$ 財の交換比率を表しています。ここで、片方の財をたくさん消費できるということは、その財のありがたみは徐々に薄まっていきます。
つまり、 $x$ 財を1単位変化させたとき、A点からB点の $y$ 財の消費量の変化よりも、B点からC点の $y$ 財の消費量の変化の方が小さくなります。
このように、無差別曲線が凸性の曲線であることは、「たくさん消費する財のありがたみはだんだん薄れていく」という消費財の特性を表し、同時に「限界代替率逓減の法則」が成り立つのです。
限界代替率逓減の法則$\\$
ある財の消費量が増加すればするほど、その財から得られる効用は低下し、もう一方の財との代替率(交換比率)が逓減すること。$\\$
性質④:異なる曲線は互いに交わらない
人々の好み(選好)は変わらないはずなので、異なる無差別曲線は交わらないとされています。
つまり、人々の嗜好は首尾一貫しているため、無差別曲線が交わるような場合には、財の好き嫌いの好みが変化したと言えます。
ここで、個人の嗜好(選好)が首尾一貫している条件として、経済学的には「完備性」や「推移性」があるとされていますが、好みがはっきりしていると理解できればOKです。
大事なのは、人々の嗜好は一貫していて、無差別曲線の異なる曲線は交わらないことを覚えましょう。
おわりに:無差別曲線は人々の好み(選好)を表すツール
無差別曲線は、各個人の好み(選好)を表すツールとなります。
この無差別曲線を使って、消費者の合理的行動(効用最大化)を明らかにしていきます。
ですから、消費者行動を分析する上で、無差別曲線は必須となるので、必ずマスターしましょう!

以上となります。参考になった方は応援もよろしくお願いします!
【参考文献】
尾山・安田(2013)『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏(2014)『ミクロ経済学の力』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】







コメント