【ミクロ経済学】限界効用とは何？【グラフと数式で図解】

こんにちは、とし（@tyobory）です。

ミクロ経済学を学ぶとき、「需要と供給」と同じくらい大事な単元として「限界効用」があります。

「限界革命」と呼ばれるように、ここから「マルクス経済学」に対して「近代経済学」の学問体系が樹立され、「マクロ経済学」や「ミクロ経済学」に分かれていくのです。

ミクロ経済学の第1回のテーマは「効用関数と無差別曲線」の「限界効用」です。

目次：効用関数と無差別曲線（消費者行動）

それでは、「限界効用」について掘り下げていきます。

限界効用とは何？【まずは概念を理解する】

「限界」とは、「効用」とは？

限界効用の「限界」と「効用」とは

限界効用を理解するには、「限界」と「効用」の概念を押さえる必要があります。

「限界」って言葉をみると、「もう無理！」・「ギリギリ」ってイメージだと思いますが、経済学では「追加的な」や「１単位変化させたとき」を意味します。

一方で、「効用」とは、「満足度」のことを指します。ここでいう「満足度」とはモノを消費したときのうれしい気持ちです（大雑把に言うと）。以下、定義です。

消費者が財・サービスを消費することで得られる満足の度合いを数量的に表したもの

ポイントは「財・サービス」を消費すること、そしてその消費から満足度を得ることです。

この「限界」と「効用」の概念を掛け合わせると、「限界効用」を理解することができます。

「限界効用」（Marginal Utility）とは

限界効用は、財・サービスを消費量を変化させたときの効用（満足度）に着目します。

キーワードは２つで、「財の消費量を変化させる」、「そのときの満足度の変分」です。

「限界（margin）」の意味として「境界線」を挙げましたが、「財の消費量の境界線をいじる」＝「財の消費量を微調整する」、これを数学的に表現すると「微分」になります。

「限界」の概念はよく出てくるので、絶対押さえておかなければならない事項です。

限界効用・限界代替率・限界収入・限界費用・限界生産性・限界評価…etc
最近の書籍では『限界費用ゼロ社会』などで使われていますよね。

限界費用ゼロ社会 〈モノのインターネット〉と共有型経済の台頭

created by Rinker

¥2,640 (2025/04/02 06:35:23時点 Amazon調べ-詳細)

• Kindle
• Amazon
• 楽天市場
• Yahooショッピング

以上、用語で「限界効用」を説明しましたが、次は図と数式で解説したいと思います。

「限界効用」のグラフと数式

グラフをかけるようになる。

限界効用のグラフと数式で理解

限界効用は英語で「Marginal Utility」といい、「MU」で表現されます。

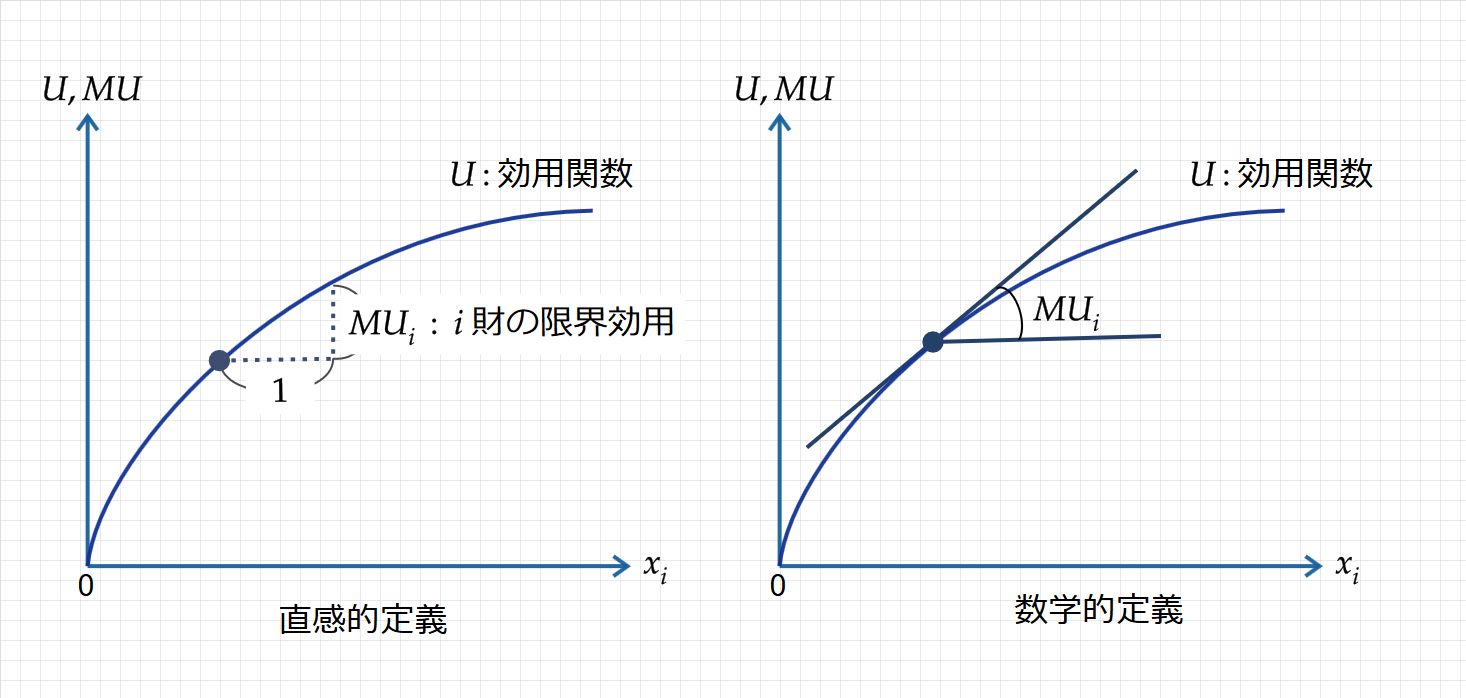
直感的定義だと、$\small x_i$財を１単位増やしたとき、効用の増加分が$\small U_i$となります。

数学的定義だと、効用関数（$\small U$）の接線の傾きの大きさ（$\small U_i$）として表されます。

つまり、

数学的には、効用関数：$\small U$はたくさんの財の消費量に依存しますが、ここでは第$\small i$財のみを変化させたときの効用の増分を表しており、第$\small i$財で微分した形になっています。

これを「偏微分」といい、第$i$財の限界効用（$\small U_i$）が求められます。
（∂は「ラウンド・ディー」と読みます）

「限界的に１単位増やす」という言葉は頻出でよく使いますので覚えておきましょう！

【補足】「限界効用」の演習問題

問題1

以下のような効用関数が与えられている。それぞれの財の限界効用を求めなさい。

①　$U=x^2y^2$
②　$U=3x^3y^4$

答え

①　$MU_x=\frac{\partial U}{\partial x}=2・x^{2-1}・y^2=2xy^2$
　　$MU_y=\frac{\partial U}{\partial y}=2・x^2・y^{2-1}=2x^2y$

②　$MU_x=\frac{\partial U}{\partial x}=3・3・x^{3-1}・y^4=9x^2y^4$
　　$MU_y=\frac{\partial U}{\partial y}=3・4・x^3・y^{4-1}=12x^3y^3$

おわりに：「限界効用」の概念を理解する

「限界」概念は、「マクロ経済学」「ミクロ経済学」を学ぶ上で、重要概念となります。

また、「限界」ときたら微分することになるので、必ず計算できるようになりましょう。

以上、「限界効用」についてでした。

以上となります。参考になった方は応援もよろしくお願いします！

【参考文献】
尾山・安田（2013）『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏（2014）『ミクロ経済学の力』日本評論社.

マクロ経済学の学習はこちら 　マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら　ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら　【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】