こんにちは、とし(@tyobory)です。
ミクロ経済学第16回テーマ「規模に関する収穫一定・逓増・逓減」です。
全体の目次:「規模に関する収穫一定・逓増・逓減」
2.規模に関する収穫逓増
2.規模に関する収穫逓減
「規模に関する収穫」という言葉だけでは、経済学で収穫?何だそれと思うかもしれません。
本記事では、「規模に関する収穫」についてグラフと数式を使って解説していきます。
規模に関する収穫一定・逓増・逓減【生産要素】

収穫?
規模に関する収穫とは何か
企業は、生産活動を行う上で、生産要素として労働や資本を投入します。
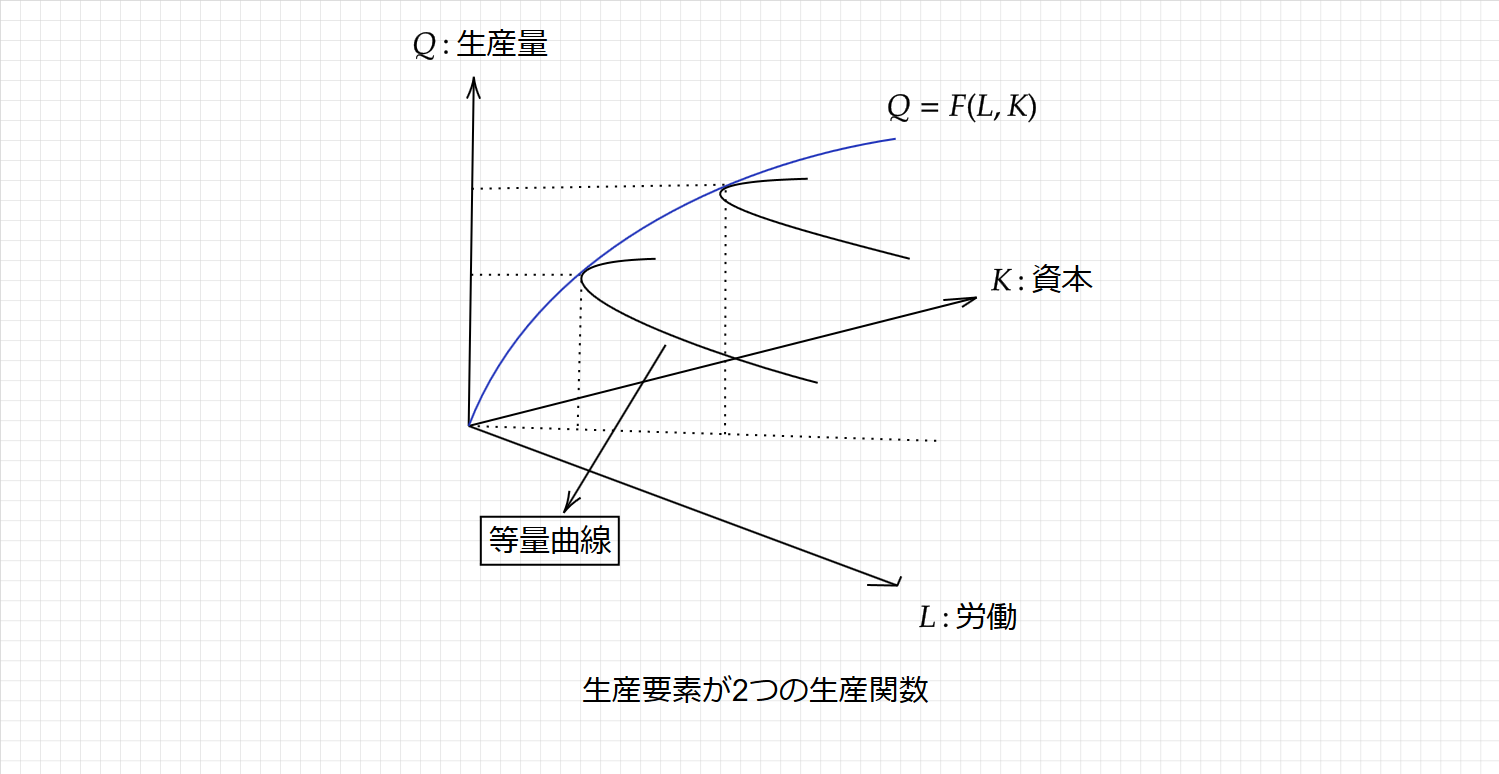
$\small Q=F(L,K)$
解釈は、労働($\small L$)と資本($\small K$)、2つの生産要素を使って生産物($\small Q$)を作る。
$\small F$や$\small f$を使うのは、「function:関数」の頭文字から取っています。
「収穫」とは生産量($\small Q$)のことで、「規模に関する」とは生産規模を増やした場合を指します。
⇒「生産規模を増やしたとき、生産量はどのように変化するか」という意味になります。
より数学的な解釈は、「各生産要素を $\small a$ 倍したら、生産量は $\small a$ 倍($\small a>1,a<1$) なるのか」です。
すべての生産要素の量が $\small a>1$ 倍になったとき
生産量もちょうど $\small a$ 倍増える:収穫一定(constant returns to scale)
生産量は $\small a$ 倍より多く増える:収穫逓増(increasing returns to scale)
生産量は $\small a$ 倍未満しか増えない:収穫逓減(decreasing returns to scale)
生産要素(労働と資本)に関して、「等量曲線と等費用曲線」の記事でご確認ください。
以下、さらに詳しく確認していきましょう。
規模に関する収穫一定
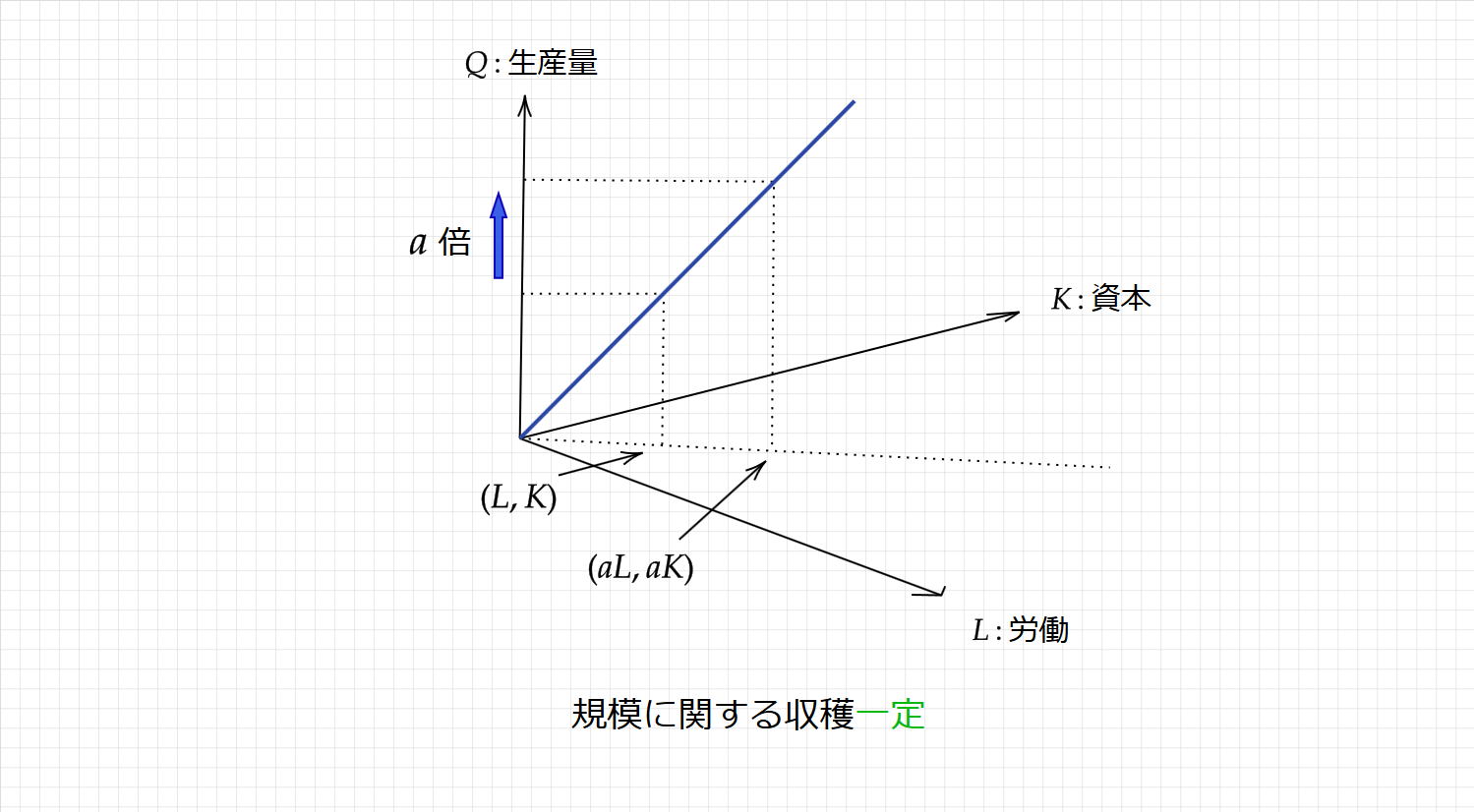
規模に関する収穫一定は、生産要素を $\small a$ 倍($\small a>1$)したら、生産量もちょうど $\small a$ 倍になることです。
$\small F(aL,aK)=aF(L,K)$
上図のように、生産要素をそれぞれ $\small a$ 倍したら、生産量も $\small a$ 倍になってます。
このとき、費用面でも、$\small a$ 倍した分だけ費用が増えます。
これが、「規模に関する収穫一定」です。
規模に関する収穫逓増
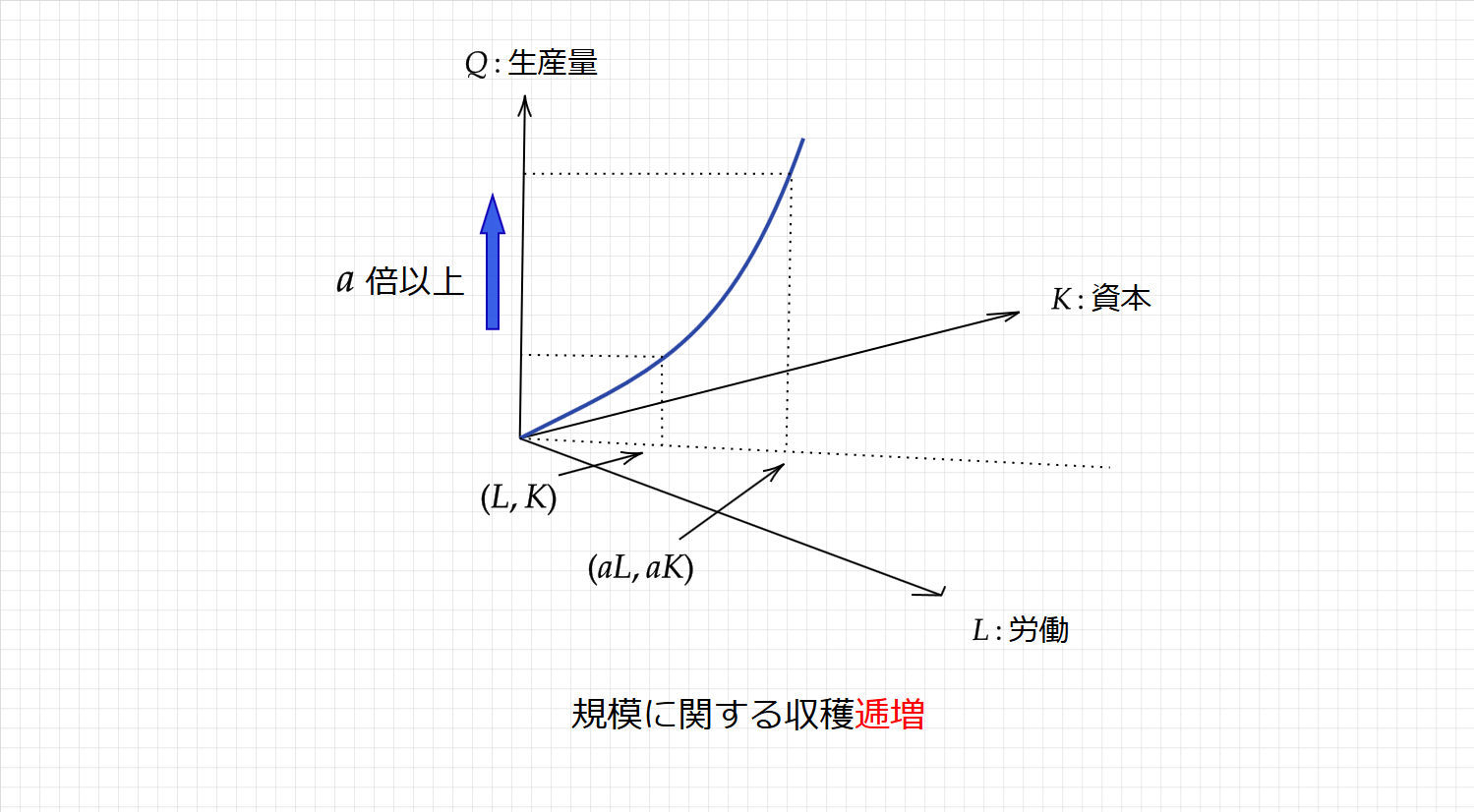
規模に関する収穫逓増は、生産要素を $\small a$ 倍($\small a>1$)したら、生産量は $\small a$ 倍よりも大きくなることです。
$\small F(aL,aK)<aF(L,K)$
上図のように、生産要素をそれぞれ $\small a$ 倍したら、生産量は $\small a$ 倍よりも大きくなっています。
収穫逓増が強く働くとき、事業を拡大すればするほど生産量に対するコストが削減されるため、大企業ほど市場を占有できるようになり、独占化されます。
これが、「規模に関する収穫逓増」です。
規模に関する収穫逓減
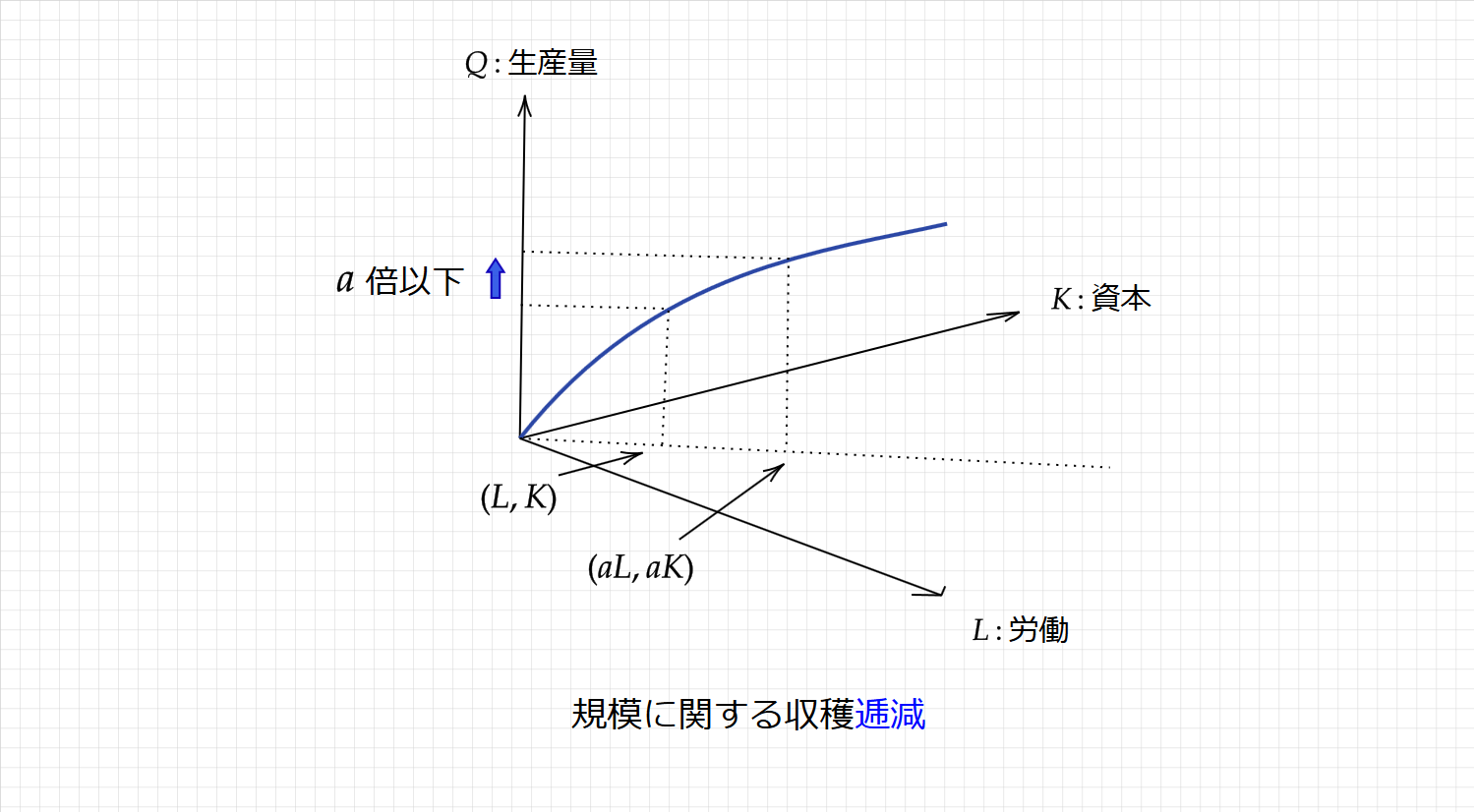
規模に関する収穫逓減は、生産要素を $\small a$倍($\small a>1$)したら、生産量は $\small a$ 倍未満にしかならないことです。
$\small F(aL,aK)>aF(L,K)$
上図のように、生産要素をそれぞれ $\small a$ 倍したら、生産量は $\small a$ 倍よりも小さくなっていますね。
収穫逓減の場合、同じコストをかけても、同倍の生産量(収穫)が得られない状況です。
通常の事業拡大では、経営資源(リソース)の共有があるため、収穫逓減はあまり起こりえないケースとされてます。
これが、「規模に関する収穫逓減」です。
【補論】「規模に関する収穫」を例題で確認する
ある企業の生産関数が次のように与えられている。
$Q=L^{0.6}K^{0.4}$
この生産関数の規模に関する収穫について、「一定」「逓増」「逓減」どれに当たるか調べなさい。
(解)
それぞれの生産要素を $\small a$ 倍すると、
$\small Q=(aL)^{0.6}(aK)^{0.4}$
$\small Q=a^{0.6}L^{0.6}\times a^{0.4}(K)^{0.4}$
$\small Q=a^{0.6+0.4}L^{0.6}(K)^{0.4}$
$\small Q=aL^{0.6}(K)^{0.4}$
以上より、$\small F(aL,aK)=aF(L,K)$が成り立ち、この生産関数は規模に関する収穫一定である。
おわりに:規模に関する収穫一定は、1次同次関数
規模に関する収穫一定となる関数は、「1次同次関数」と呼びます。
関数$\small F(x,y)$が任意の実数$\small x$、$\small y$、$\small t$に対して
$\small F(tx,ty)=t^m(x,y)$
が成り立つとき、$\small F(x,y)$を$\small m$次同次関数という。
1次同次なら、$\small a$ 倍したら、ちょうど$\small a$ 倍、2次同次なら $\small a^2$ 倍になるといった感じです。
以上、「規模に関する収穫」についてでした。

参考になった方は応援もよろしくお願いします!
【参考文献】
尾山・安田(2013)『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏(2014)『ミクロ経済学の力』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】




コメント