こんにちは、とし(@tyobory)です。
ミクロ経済学の「効用関数と無差別曲線」の第3回です。
目次:効用関数と無差別曲線(消費者行動)
第1回では「限界効用」、第2回では「無差別曲線」について学びました。
まだ、「限界効用」や「無差別曲線」って何?という人は下記記事をご参考ください。
第3回のテーマは「限界代替率(MRS)」で、これまでの内容を踏まえた上で説明していきます。
【ミクロ経済学】限界代替率とは?【グラフと数式で解説】

限界代替率とは…?
限界代替率(Marginal Rate of Substitution)とは
限界代替率は英語で「Marginal Rate of Substitution:$\small MRS$」と呼ばれます。
限界代替率を理解するには、「限界」と「代替率」に分けて考えると分かりやすいです。
限界:追加的に1単位増やす
代替:2財の交換( $x$ 財と $y$ 財の交換)
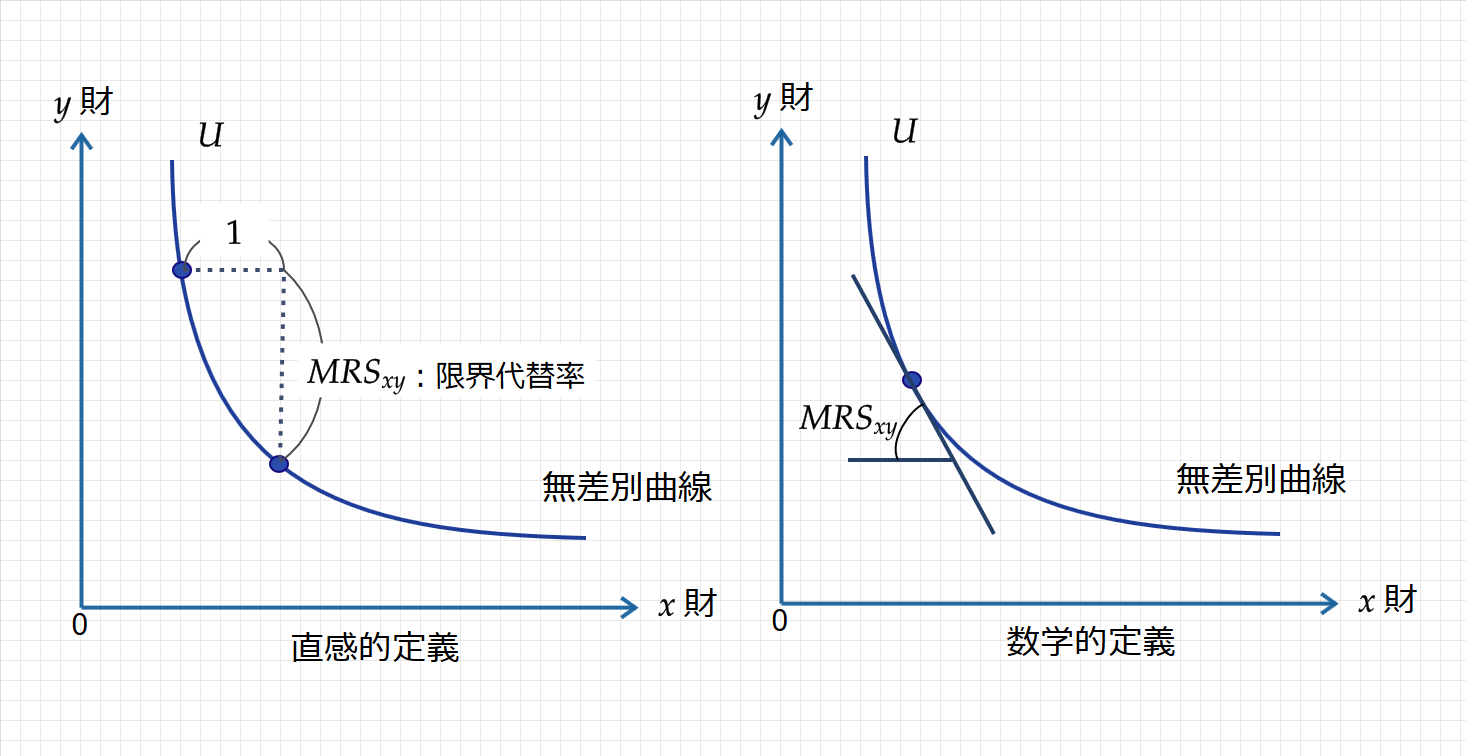
直感的定義: $x$ 財を1単位増やすために、支払っても良い $y$ 財の消費量
数学的定義:無差別曲線の接線の傾き
このように、限界代替率とは、「ある財の消費量を追加的に1単位増やす交換として、支払ってもよいと考えているもう一つの財の消費量」である。
ざっくりまとめると、 $x$ 財を増やすから、等価交換で $y$ 財は諦めてね!って感じです。
限界代替率逓減の法則
無差別曲線の性質から「限界代替率逓減の法則」が成り立つことを過去記事でもまとめていますが、少し復習です。
限界代替率は無差別曲線の接線の傾きで表されます。ここで、片方の財をたくさん消費できるということは、その財のありがたみは徐々に薄まっていきます。
つまり、 $x$ 財の消費量を1単位変化させたとき、A点からB点の $y$ 財の消費量の変化よりも、B点からC点の $y$ 財の消費量の変化の方が小さくなっていますよね。
このように、無差別曲線が凸性の曲線であることは、「たくさん消費する財のありがたみはだんだん薄れていく」という消費財の特性を表すとともに、「限界代替率逓減の法則」が成り立つのです。
限界代替率逓減の法則$\\$
ある財の消費量が増加すればするほど、その財から得られる効用は低下し、もう一方の財との代替率(交換比率)が逓減すること。$\\$
限界代替率を数式で考える【各財の変化量】
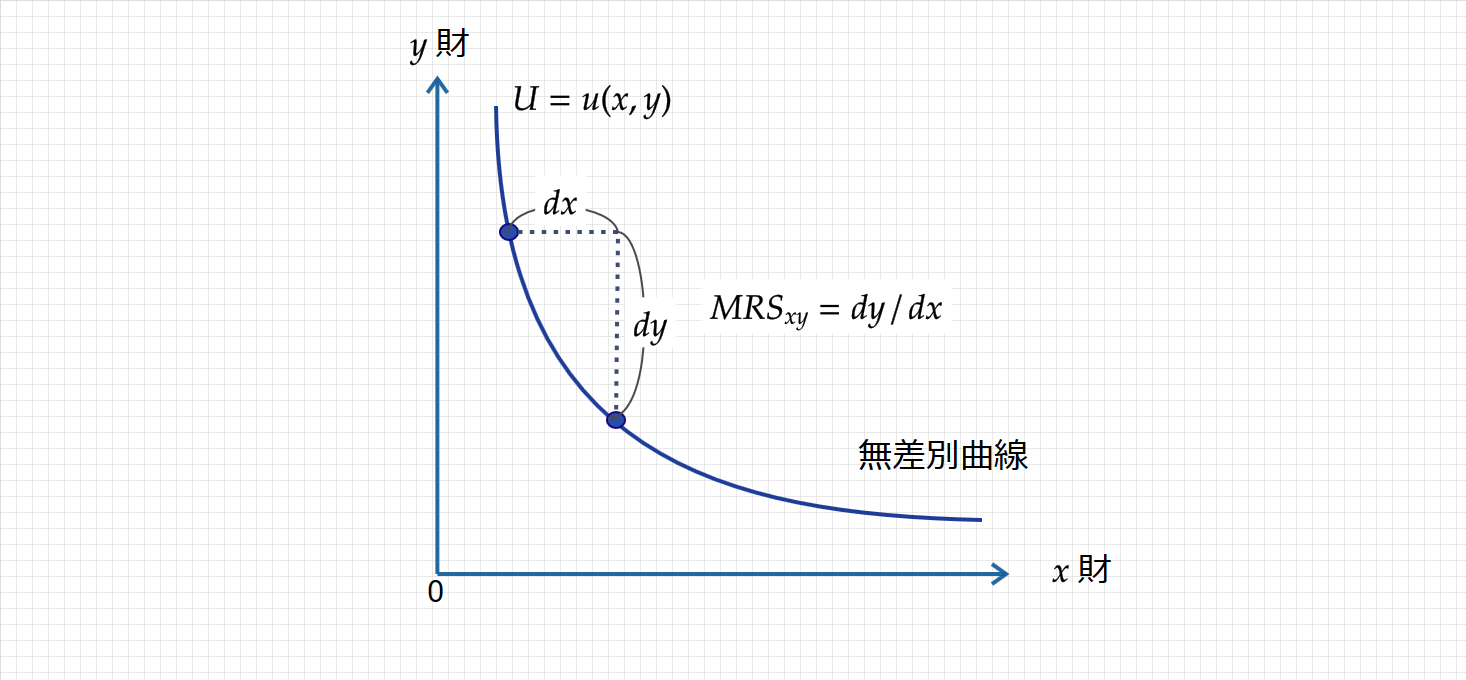
次に、 $x$ 財と $y$ 財の消費量の変化に着目して見てみましょう。
限界代替率(MRS)は無差別曲線の接線の傾きで表されます。
つまり、$x$ 財と $y$ 財の消費量の変化は $dx$ と $dy$ で示され、傾きの大きさは
$$\small MRS_{xy}=\frac{dy}{dx}$$
となります。この他に、限界代替率の傾きの大きさを導出する方法があります。
限界代替率を数式で考える【限界効用】
各財の効用の変化に着目します。今、効用を一定に保つため、$x$ 財の消費量を増やし、 $y$ 財の消費量を減らしています。
つまり、全体の効用の変化量は次のように示されます。
$$\small du=\frac{\partial U}{\partial x}・dx+\frac{\partial U}{\partial y}・dy$$
数式がよく分からない!という人がいるかもしれませんが、よくよく見ると $\frac{\partial U}{\partial x}$ は $x$ 財の限界効用($\small MU_x$)です。
$\frac{\partial U}{\partial x}$: $x$ 財が1単位変化したときの効用の変化量(=限界効用$\small MU_x$)
$\small dx$ : $x$ 財の変化量
$\small \frac{\partial U}{\partial x}$×$\small dx$: $x$ 財の消費量が変化したときの効用の変化量
$y$ 財も同様です。つまり、$du$ は $x$ 財の消費量が変化したことによる効用の変化量と $y$ 財の消費量が変化したことによる効用の変化量を足し合わせたものです。
ただし、無差別曲線と限界代替率の定義から、無差別曲線上は効用水準が等しいため、効用水準の変化はありません($du=0$)。したがって、それぞれの限界効用を$\small MU_x$, $\small MU_y$ とすると、
$$\small du=MU_x・dx+MU_y・dy=0$$
$$\small -\frac{dy}{dx}=\frac{MU_x}{MU_y}$$
となり、どこかで見たような数式となりました。
以上より、限界代替率($\small MRS$)の絶対値をとると、
おわりに:数式の部分が難しいかもしれませんが…
消費者行動を分析する上で、限界効用・無差別曲線・限界代替率の考え方は、形を変えて何度も出てきます。
また、これらをベースに予算制約時の最適消費理論が展開されているので、必ずマスターしましょう!

以上となります。参考になった方は応援もよろしくお願いします!
【参考文献】
尾山・安田(2013)『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏(2014)『ミクロ経済学の力』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】






コメント