こんにちは、とし(@tyobory)です。
ミクロ経済学の第1回から第7回まで「消費者理論」について取り扱いました。まだ未学習!の方は、次の記事を参考にページに飛んで頂けたら幸いです。

今回のテーマから「企業の生産者理論」を取り扱います。第8回のテーマは「生産関数と総費用」です。以下、全体の目次です。
目次:「生産関数と総費用」
2.生産関数(労働と資本)、限界生産力($\small MP$)
3.総費用関数(可変費用と固定費用)
生産者理論は企業行動を明らかにすることを目的としています。結論から言うと、企業は利潤を最大化するように行動します。本記事では、企業の生産について生産関数を定義し、各用語を確認していきます。
【ミクロ経済学】生産関数と限界生産力【労働と資本】
利潤、生産関数を定義する。
企業行動と生産者の利潤【利潤、総収入、総費用】
ミクロ経済学において、企業は自社の利潤を最大化するように行動すると考えられています。つまり、これをモデル式で簡単に表すと次のようになります。
― 生産者の利潤 ―
$\small \Pi = TR-TC=P \times Q -(VC+FC)$
( $\small \Pi$:利潤、$\small TR$:総収入、$\small TC$:総費用、
$\small P$:価格、$\small Q$:生産量、$\small VC$:可変費用、$\small FC$:固定費用 )
総収入($\small TR:Total\,Revenue$):企業が財やサービスを売って得られる収入の総額
総費用($\small TC:Total\,Cost$):企業が財やサービスを生産するのに必要な費用の総額
可変費用($\small VC:Variable\,Cost$):生産量に応じて生じる費用
固定費用($\small FC:Fixed\,Cost$):生産量に関わらず生じる費用
総収入($\small TR$)は 財の価格に生産量を乗じた$\small PQ$で示され、総費用($\small TC$)は生産量に応じて生じる可変費用($\small VC$)と生産量に関わらず生じる固定費用($\small FC$)で表されます。
可変費用($\small VC$)は、生産量に応じてかかる費用のことで、原材料の調達など、生産量が増えるとその分費用も変化します。一方、固定費用($\small FC$)は、土地代・店舗賃貸料など、財やサービスの生産がゼロでも発生する費用のことです。
以上のように、利潤は総収入から総費用を差し引くことにより導出されます。
生産関数と生産要素(S字型曲線)
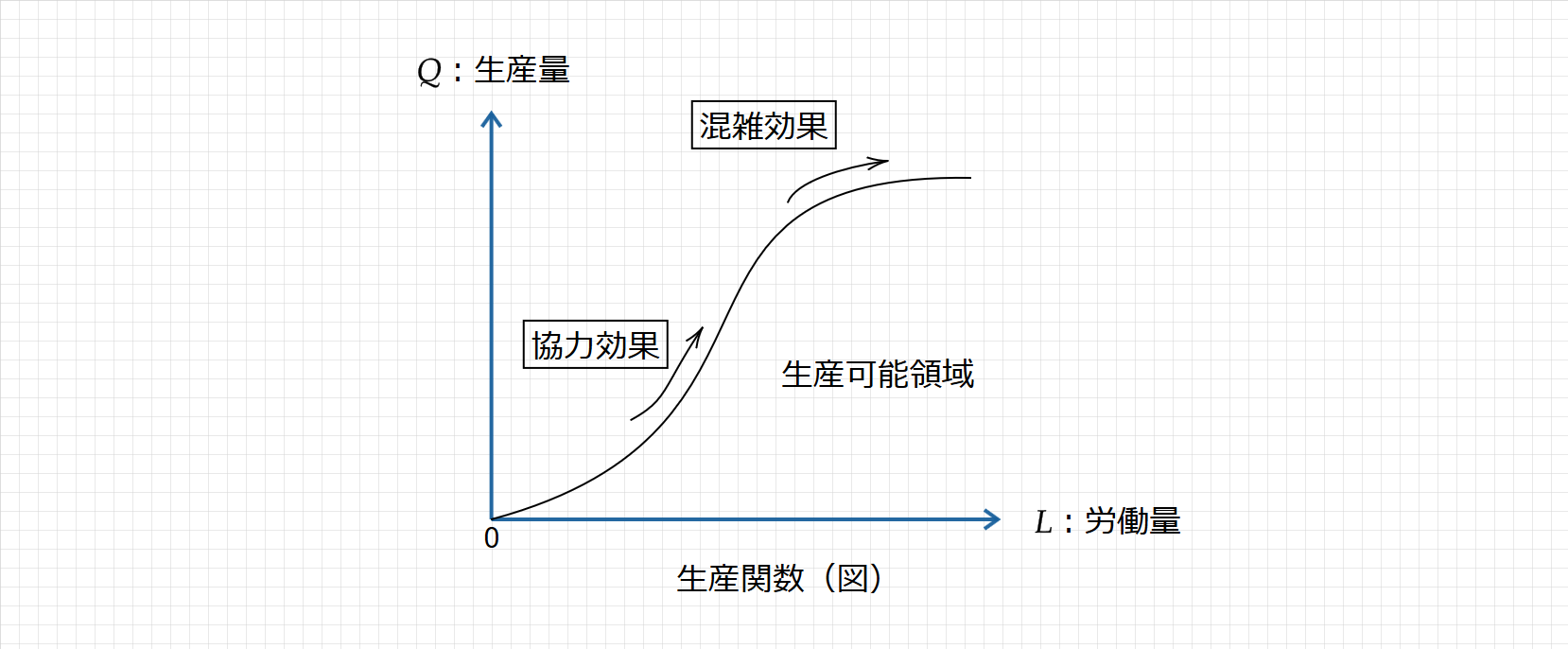
企業は生産要素(労働と資本)を使い、どれだけの生産ができるか考えます。まず、生産関数は次のように図示されます。
資本Kを固定し、生産要素を労働(L)のみとした生産関数を考えていきます。
まず、労働量が増加すると生産量も増加するため、生産関数は右上がりの曲線となります。ここで、生産量が少ないうちは協力効果が発生するため、限界生産力が逓増します。
しかし、ある地点から労働力に対する混雑効果が発生し、限界生産力は徐々に逓減していくことになります。このように、生産関数は一般的にS字型の曲線で示されます。
生産関数と限界生産力(MPLとMPK)
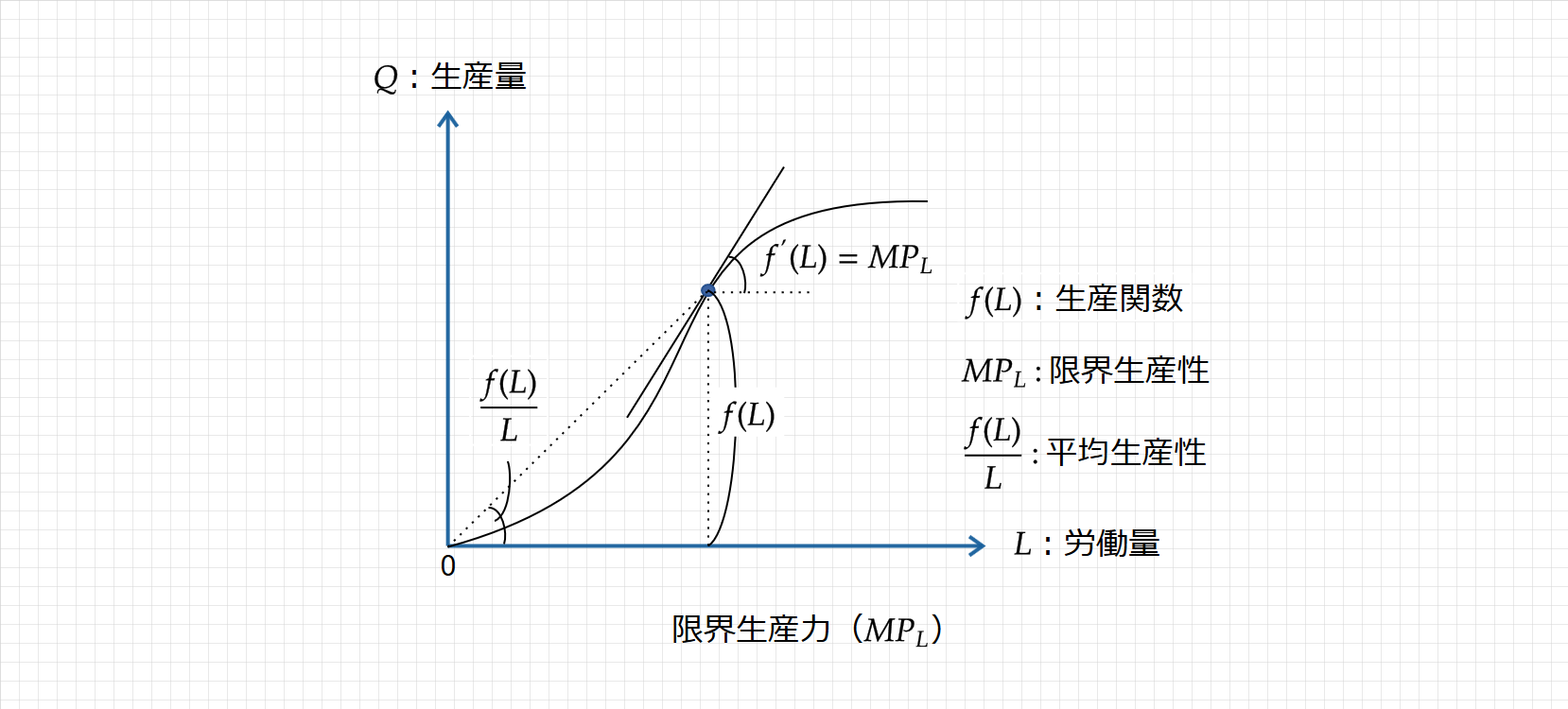
さらに、生産関数のグラフを掘り下げると、下記のように解釈できます。
$\small Q=f(L)$:生産関数 $\\$ $\small MP_L$:限界生産力;労働量を1単位変化させたとき、生産量がどれくらい変化するか $\\$ $\small \frac{\displaystyle f(L)}{\displaystyle L}$:平均生産性;労働力1単位当たりの生産量
現在、生産要素はLのみであるため、生産関数は労働(L)の関数となる。ここで、生産関数を労働(L)で微分すると、その接線の傾きの大きさは限界生産力であり、これを労働の限界生産力($\small f'(L)=MP_L$)といいます。
他方で、仮に生産要素が二つの場合、もう一つの生産要素である資本は生産関数を資本(K)で微分することにより、資本の労働生産力($\small MP_K$)が導かれます。以上をまとめると…
労働の限界生産力:$\small MP_L=\frac{ΔQ}{ΔL}$
資本の限界生産力:$\small MP_K=\frac{ΔQ}{ΔK}$
このように、限界生産力は各生産要素で微分した接線の傾きの大きさとして示されます。
【ミクロ経済学】生産関数と総費用曲線【逆S字型曲線】

生産関数から総費用曲線を導出。
総費用曲線の導出(逆S字型曲線)
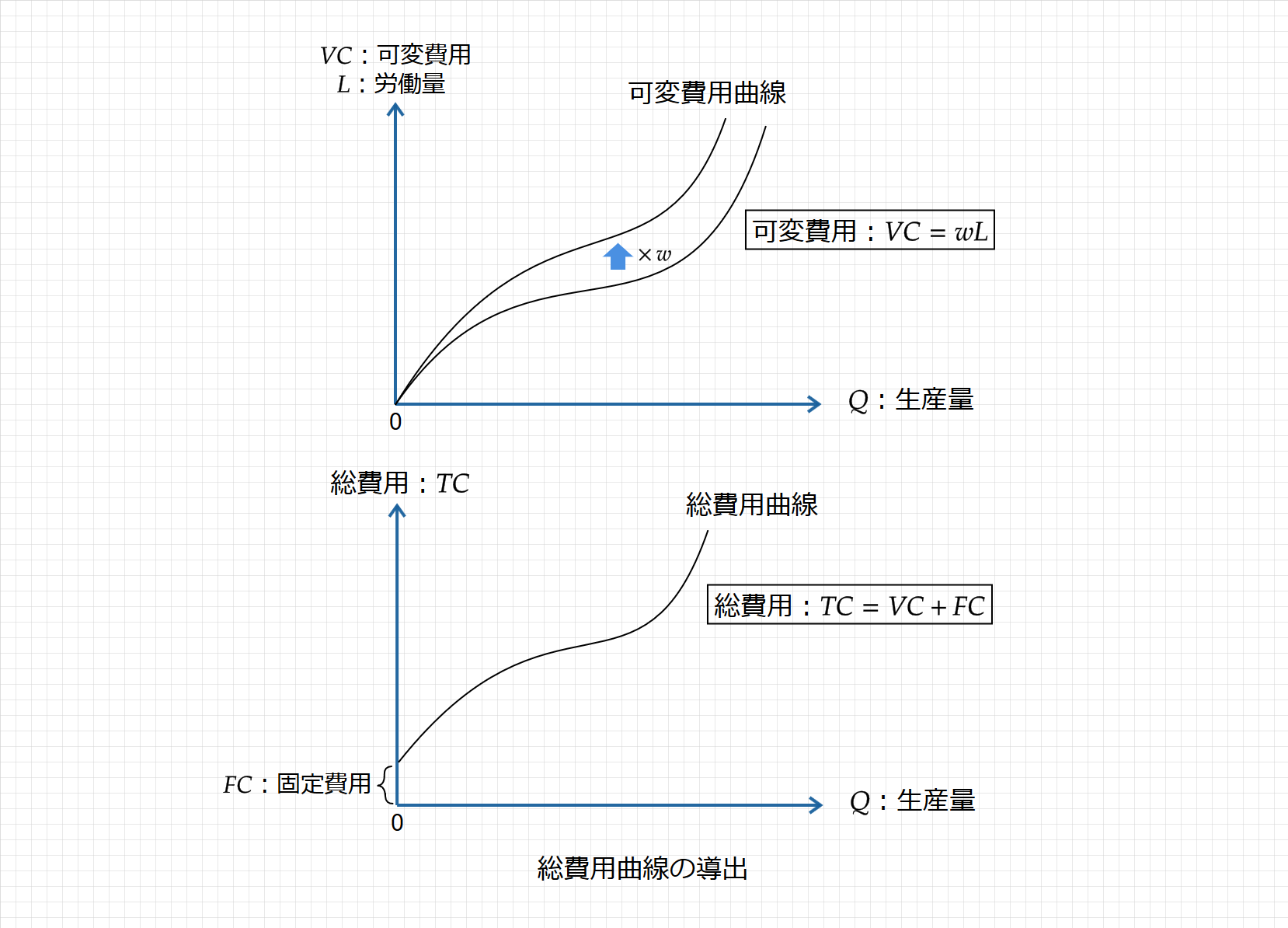
総費用曲線は生産関数のグラフから導きだすことができます。
まず、生産関数の曲線を反転させ、賃金($\small w$)を乗じると、労働量($\small L$)に応じた可変費用曲線($\small VC$)が導出されます。ここで、総費用($\small TC$)とは可変費用($\small VC$)に固定費用($\small FC$)を上乗せしたものなので、総費用曲線は可変費用曲線に固定費用を加えた曲線として示されます(下図)
総費用曲線の接線は限界費用($\small MC$)であり、接線の傾きの大きさとして示されます。生産関数の図と解釈を対応させると、限界生産量が逓増しているとき、協力効果が発生し、生産量における限界費用が逓減します。
そして、ある地点から労働力に対する混雑効果が発生し、限界生産力が逓減するため、生産における限界費用は逓増していきます(接線の傾きが再び大きくなる)。
以上より、生産関数がS字型の生産関数ならば、総費用曲線は逆S字型の曲線で表される(もちろん、生産関数はS字型以外にも、直線や曲線など色々な形があります)。
【補論】生産関数と利潤最大化(等利潤曲線)
生産要素が労働のみの場合、利潤関数は次のように示されます。
― 生産者の利潤 ―
$\small \Pi = TR-TC=p・f(L) -wL$
( $\small \Pi$:利潤、$\small TR$:総収入、$\small TC$:総費用、
$\small p$:価格、$\small f(L)$:生産量、$\small L$:労働量、$\small w$:賃金 )
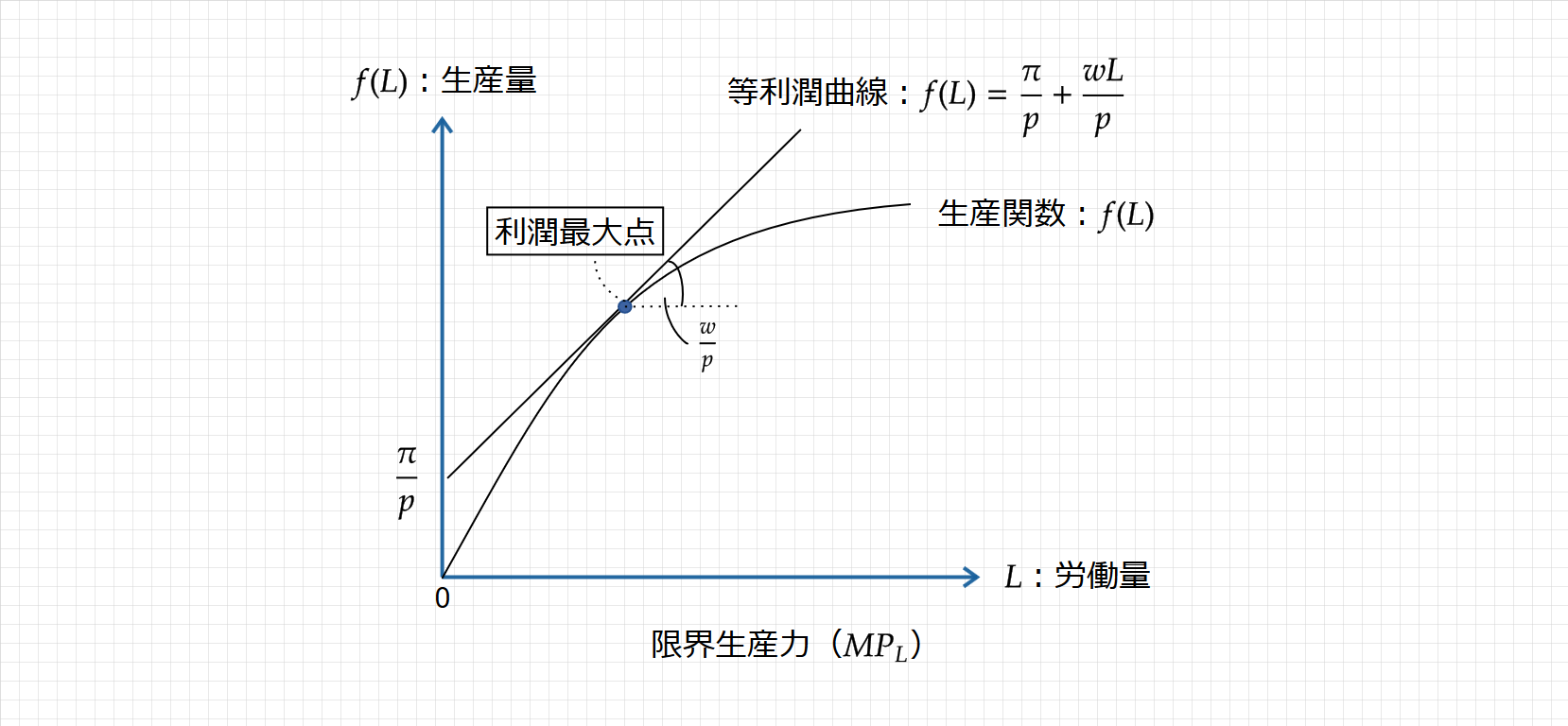
つまり、縦軸に生産量($\small f(L)$)、横軸に労働量($\small L$)をとると、次のように図示されます。
ここで、利潤を最大化させる労働量($\small L$)を考えます。つまり、利潤関数($\small \pi$)を労働量($\small L$)で微分すると…
$\small \frac{\displaystyle Δ\Pi}{\displaystyle ΔL}= p・f'(L) -w=0$
$\small f'(L) =\frac{\displaystyle w}{\displaystyle p}$
利潤最大化条件は労働の限界生産力($\small f'(L)$)と実質賃金($\small \frac{\displaystyle w}{\displaystyle p}$)が等しいとき
等利潤曲線と生産関数の曲線が接するとき、つまり労働の限界生産力と実質賃金が等しいときに利潤最大化が達成される。
おわりに:利潤関数を正しく理解する
企業における生産者理論は利潤関数からすべて始まります。
価格(P)、生産関数(Q)、総収入(TR)、総費用(TC)など、一つ一つの概念を定義し、図式化されていきます。
利潤関数はその原点になるので、正しく理解していきましょう。

以上となります。参考になった方は応援もよろしくお願いします!
【参考文献】
尾山・安田(2013)『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏(2014)『ミクロ経済学の力』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】




コメント