こんにちは、とし(@tyobory)です。
マクロ経済学第3回テーマは「貯蓄関数」についてです。
今回の目次:「貯蓄関数」
2.限界貯蓄性向(Marginal propensity to save)
3.平均貯蓄性向(Average propensity to save)
前回の消費関数の続き論点となりますので、下記の記事を合わせてどうぞ!
「貯蓄関数」はマクロ経済学における総需要を考える際に、「投資と貯蓄」の論点でたびたび出題されます。前回の消費関数と同様にグラフと数式を理解していきましょう。
【マクロ経済学】貯蓄関数とは何か【理論モデルをグラフと数式で解説】

「貯蓄」とは、「消費」の反対概念である。
貯蓄関数とは何か(理論モデル)
一国の所得水準が変化したとき、貯蓄がどのように変化するのかを考えます。まず、消費関数のモデルと合わせて確認しましょう。
基礎消費($\small c_o$):所得とは無関係に生活するのに必要不可欠な消費部分
限界消費性向($\small c_1$):追加的に1単位所得が増加したとき、消費がどれだけ増加するか
限界貯蓄性向($\small 1-c_1$):追加的に1単位所得が増加したとき、貯蓄がどれだけ増加するか
貯蓄関数は消費されない部分はすべて貯蓄に回ると考えるため、貯蓄(S)は国民所得(Y)から消費(C)を差し引いた金額として定義されます。
数式を解くと、貯蓄関数の切片は $\small -c_o$ 、傾きは $\small 1-c_1$ となります。
以上が貯蓄関数の理論モデルです。
貯蓄関数をグラフで確認する
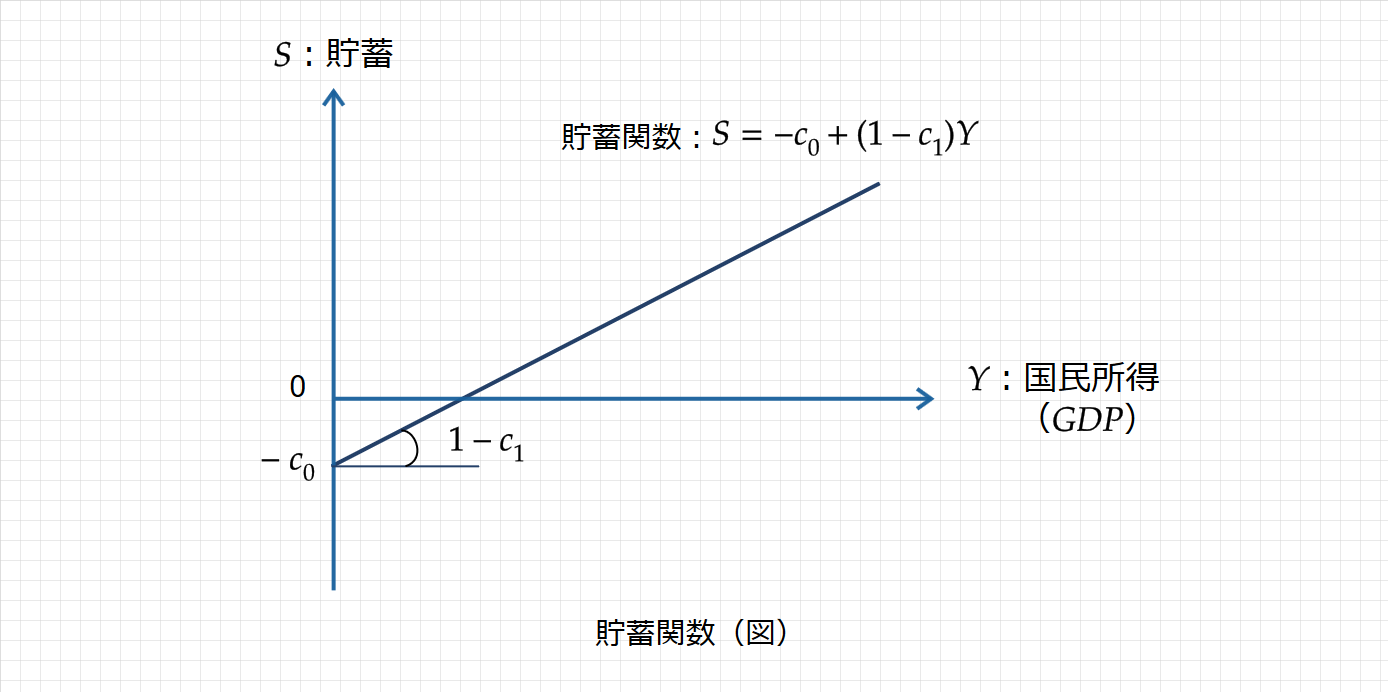
貯蓄関数をグラフにすると次のようになります(下図)。
国民所得($\small Y$)が増加すると、貯蓄($\small S$)も増加するため、これを「貯蓄($\small S$)は国民所得($\small Y$)の増加関数」といいます。
ここで、国民所得が仮にゼロのとき、所得とは無関係に支出される基礎消費($c_o$)があるため、基礎消費分マイナスとなります。
そして、国民所得が1単位増加すると、貯蓄は限界貯蓄性向($\small 1-c_1$)だけ増加します。
これがマクロ経済学における「貯蓄」についてです。
【マクロ経済学】消費関数における限界消費性向と平均消費性向を理解する
「限界貯蓄性向」と「平均貯蓄性向」を押さえる。
限界消費性向を数式で理解
限界貯蓄性向は $\small 1-c_1$ として直感的に見てきましたが、数学的に示すと次のようになります。
$\small S=-c_0+(1-c_1)Y$$\\$$\small \frac{\displaystyle ⊿S}{\displaystyle⊿Y}=1-c_1$
貯蓄関数($\small S$)を国民所得($\small Y$)で微分することにより、限界貯蓄性向($\small 1-c_1$)が求められ、貯蓄関数の接線の傾きとして示されます。
以上、限界貯蓄性向の定義と数式となります。
平均貯蓄性向とは何か【グラフと数式で理解】
貯蓄関数の論点でも、限界貯蓄性向の他に、平均貯蓄性向という概念があります。
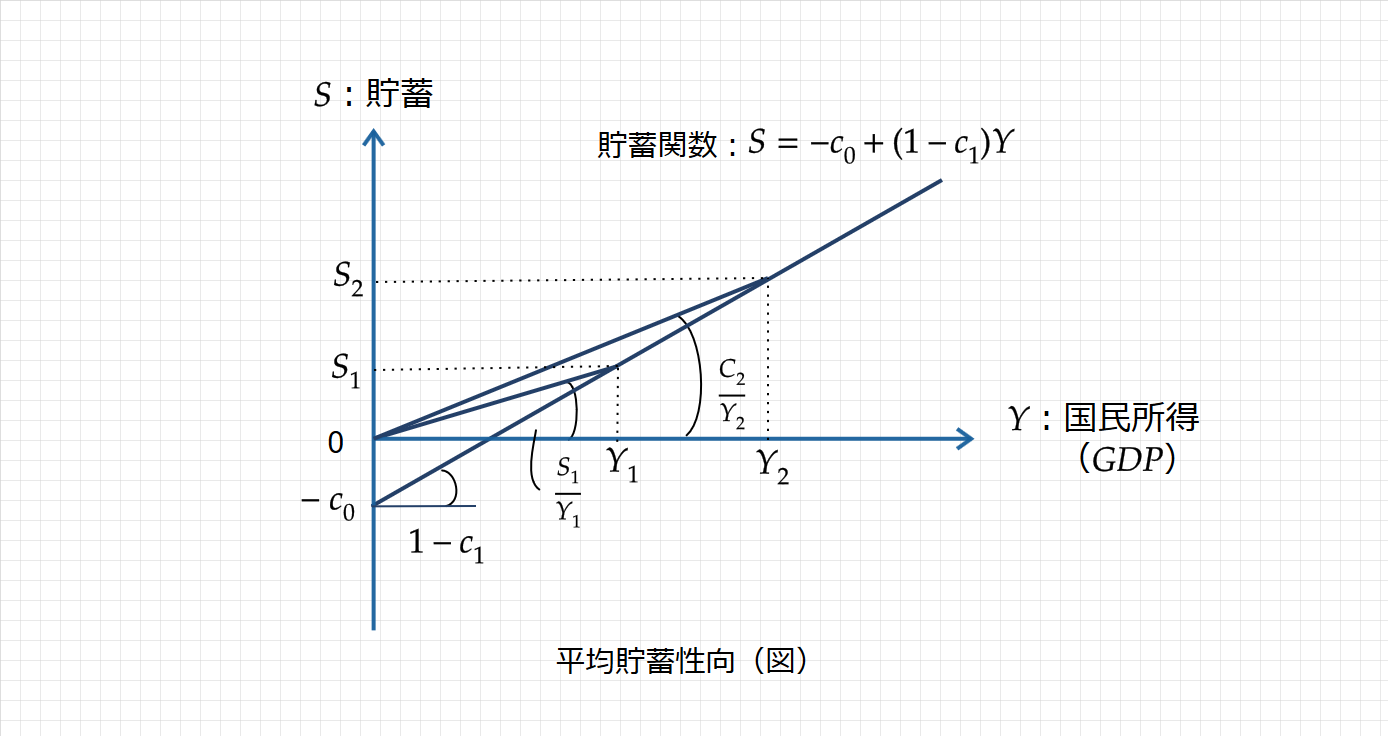
貯蓄($\small S$)を国民所得($\small Y$)で除した値が「平均貯蓄性向」となります。「平均貯蓄性向」を図示すると次のように表されます(下図)。
平均貯蓄性向は、原点と貯蓄関数上の各点を結んだ直線の傾きとして表され、次のような数式で示される。
$\small S=-c_o+(1-c_1)Y$$\\$$\small \displaystyle \frac{S}{Y}=\displaystyle \frac{-c_o+(1-c_1)Y}{Y}$
国民所得が増加すると、貯蓄も限界貯蓄性向だけ増加し、平均貯蓄性向は大きくなります。
図でも、国民所得が $\small Y_1$ から $\small Y_2$ に増加すると、平均貯蓄性向は $\small \displaystyle \frac{S_1}{Y_1}$ から $\small \displaystyle \frac{S_2}{Y_2}$ へ徐々に大きくなっていることが確認できます。
これは、限界貯蓄性向が平均貯蓄性向よりも大きいことを意味しており、Yが無限大のとき、平均貯蓄性向と限界貯蓄性向が一致します($\small Y$が無限大のとき、$\small \displaystyle \frac{-c_o}{Y}$ がゼロに近づくため、$\small 1-c_1$ と一致する)。
おわりに:消費関数と貯蓄関数は併せて理解
マクロ経済学において、「消費関数」と「貯蓄関数」は対の概念となります。
今回の復習です。
1.貯蓄関数:$\small S=-c_o+(1-c_1)Y$ $\small (0<c_o\, ,\,0<c_1<1)$
2.限界貯蓄性向:$\small \displaystyle \frac{⊿S}{⊿Y}=1-c_1$
3.平均貯蓄性向:$\small \displaystyle \frac{S}{Y}=\frac{- c_o+(1-c_1)Y}{Y}=\displaystyle \frac{- c_o}{Y}+(1-c_1)$
国民所得の決定理論において、両方の関数を使って総需要を説明しますので、併せて覚えましょう!

以上となります。参考になった方は応援もよろしくお願いします!
【参考文献】
中谷巌(2021)『入門マクロ経済学〔第6版〕』日本評論社.
齋藤誠他(2016)『マクロ経済学 新版』有斐閣.
大竹文雄(2007)『スタディガイド 入門マクロ経済学(第5版)』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】






コメント