こんにちは、とし(@tyobory)です。
ミクロ経済学第12回テーマは「最適労働供給」です。
全体の目次:「最適労働供給」
2.最適労働供給と予算制約式(公式)
3.最適労働供給の条件(余暇と労働)
4.名目賃金の上昇と屈折した労働供給曲線
最適労働供給は、最適消費の応用で、基本的な考え方は一緒です。
まだチェックしてない!って方は、下記記事をご参考ください。
本記事では、最適労働供給の決定について掘り下げていきます。
最適労働供給の決定【予算制約式と公式で図解】

最適労働供給の予算制約式をたてるようになる。
最適労働供給とは
最適消費のモデルでは、所得(Income)が与えられた状態でした。
しかし、私たちは「働く」か「休み」を選択し、働いた分だけ労働所得を得ます。
「働く」=「労働」
「休み」=「余暇(レジャー)」
まず、一般均衡モデルの予算制約式は次のように、簡略化して示されます。
支出( $\small p・C$ )=労働所得( $\small w・L$ )
P:価格、C:消費財、w:名目賃金、L:労働供給量
ここでの解釈は、労働所得は財・サービスを購入して、全額支出されることを示しています。
次に、「余暇(レジャー)」の概念を取り入れ、予算制約線がどのように図示されるか考えます。$\\$
最適労働供給と予算制約式(公式)
基本的に労働供給量は未知の変数で表され、1日24時間を振り分けることを想定します。
L:労働、l:余暇(レジャー)
労働供給量は、1日24時間から余暇(l)を差し引いた時間として表されます。
単純化のため、余暇以外の時間はすべて労働していると仮定します。
予算制約式に代入すると、
$\small p・C$ = $\small w(24-l)$
$\small C$ = $\small \frac{\displaystyle w}{\displaystyle p}(24-l)$
$\small C$ = $\small \frac{\displaystyle 24w}{\displaystyle p}-\frac{\displaystyle wl}{\displaystyle p}$
これが最適労働供給における予算制約式である。$\\$
最適労働供給の条件と屈折労働供給曲線

名目賃金の上昇は労働供給にどう影響があるのか。
最適労働供給の条件(余暇と労働を図で理解)
縦軸に消費財:C、横軸に余暇:lと置くと、最適労働供給は次のように図示されます。
予算制約線の傾きは$\frac{w}{p}$、切片が$\frac{24w}{p}$の直線で示されます。
消費財と余暇の最適労働供給条件は、最適消費の考え方と同じです
$\small MRS=MU_l/MU_C=w/p$
$\small MU_l$:余暇の限界効用
(=労働の限界不効用)
$\small MU_C$:消費の限界効用
$\small w/p$:実質賃金
ここでの解釈は、「賃金は労働の限界不効用に比例する」ということです。
つまり、労働は嫌なモノだから、限界不効用が大きい(労働が増えると、満足度が下がる)とき、高い賃金を支払う必要があります。
一方で、もっと働きたい(労働の限界不効用が小さい)とき、安い賃金でも働きます。
以上のように、最適労働供給は、無差別曲線と予算制約線が接する点 $\small E^*$で決定されます。$\\$
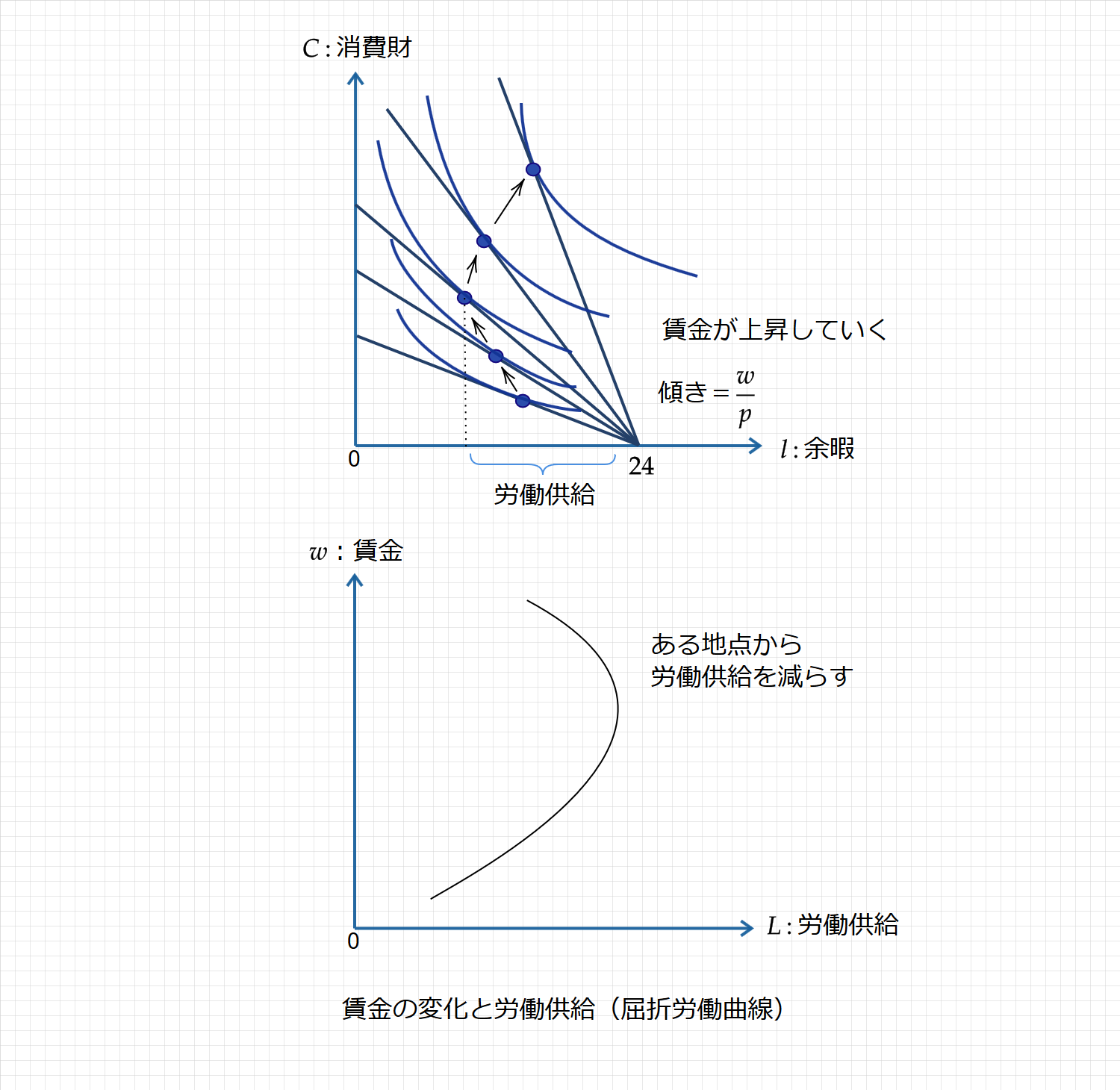
名目賃金の上昇と屈折した労働供給曲線
最後に、名目賃金が変化したとき、労働供給がどのように変化するか確認します(下図)。
はじめは賃金の上昇により、労働供給量を増やします。
しかし、ある程度賃金が高くなると、今度は余暇の機会費用が高くなるため、ある地点から労働供給量は減っていきます。
(要は、これ以上働きたくないでござる状態)
このように、賃金の上昇と労働供給を図示すると、労働供給曲線は屈折した曲線で示されます。$\\$
おわりに:最適労働供給の決定も、考え方は「最適消費」と一緒
最適労働供給の決定についても、考え方は「最適消費」と同じです。
パターンを覚えておけば、以前にも見たことある!ってことが結構あるので、まとめて直感的に覚えていくのがコツです。
以上、最適労働供給の決定でした。

以上となります。参考になった方は応援もよろしくお願いします!
【参考文献】
尾山・安田(2013)『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏(2014)『ミクロ経済学の力』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】





コメント