こんにちは、とし(@tyobory)
ミクロ経済学第14回のテーマは「等量曲線と等費用曲線」です。
全体の目次:「等量曲線と等費用曲線」
2.技術的限界代替率(MRTS)
3.等費用曲線
4.費用最小化
生産者理論でも、消費者理論の無差別曲線と同じような、凸型の曲線があります。これを「等量曲線(等産出量曲線)」といいます。
以下、キーワードの等量曲線・等費用曲線・費用最小化・技術的限界代替率を掘り下げていきます。
等量曲線と技術的限界代替率(MRTS)とは

等量曲線を正しく理解する。
等量曲線とは【労働と資本の組み合わせ】
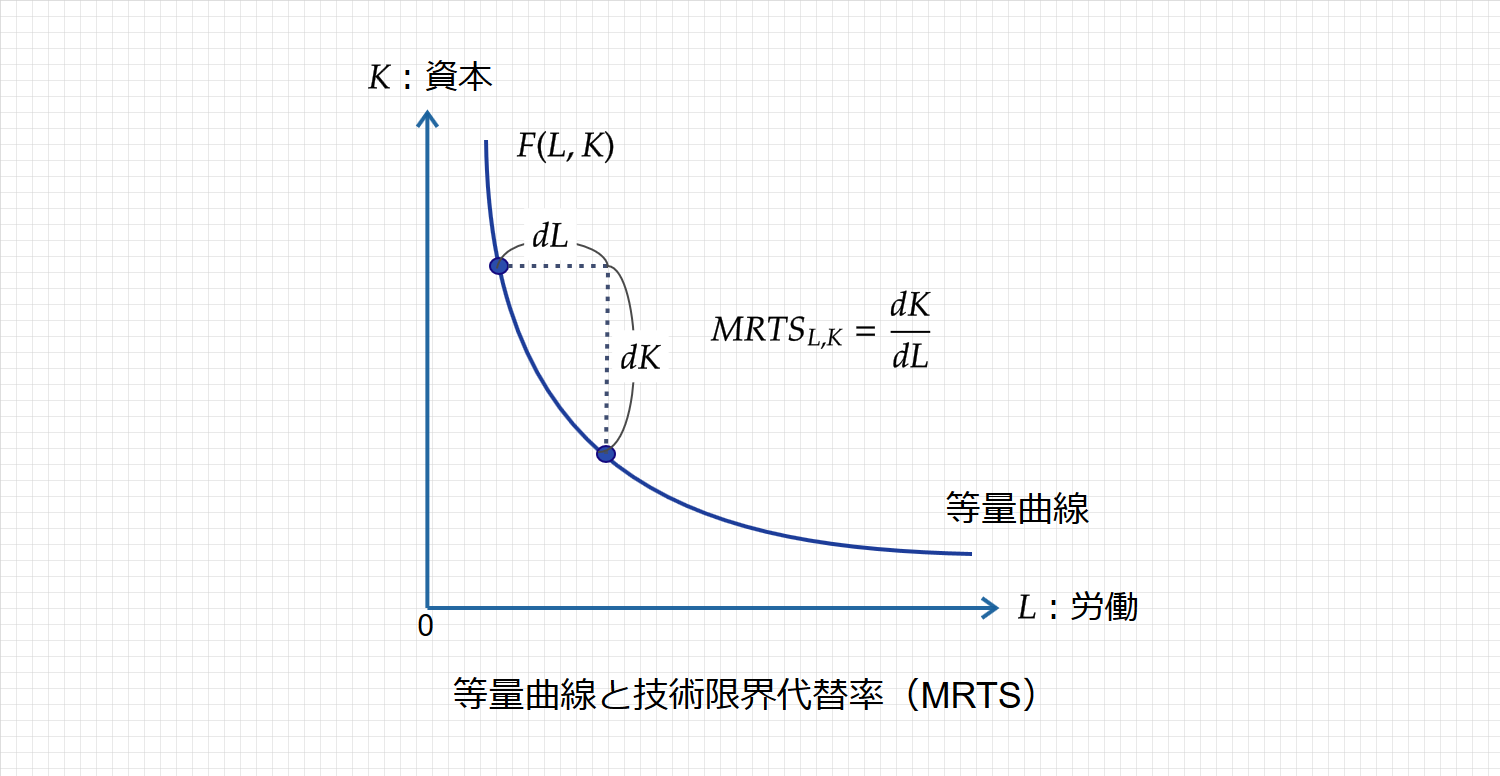
等量曲線は、一定の生産量を達成するための労働と資本の組み合わせの軌跡です(下図)。
等量曲線は無差別曲線と同様の性質があります。
① 右上方に位置するほど生産量が大きくなる
② 労働量が増加すると、労働の限界生産性は低下する
=(限界生産力逓減の法則)
このように、労働量が増加するにつれて、節約できる資本量は減少していきます。
等量曲線と技術的限界代替率(MRTS)
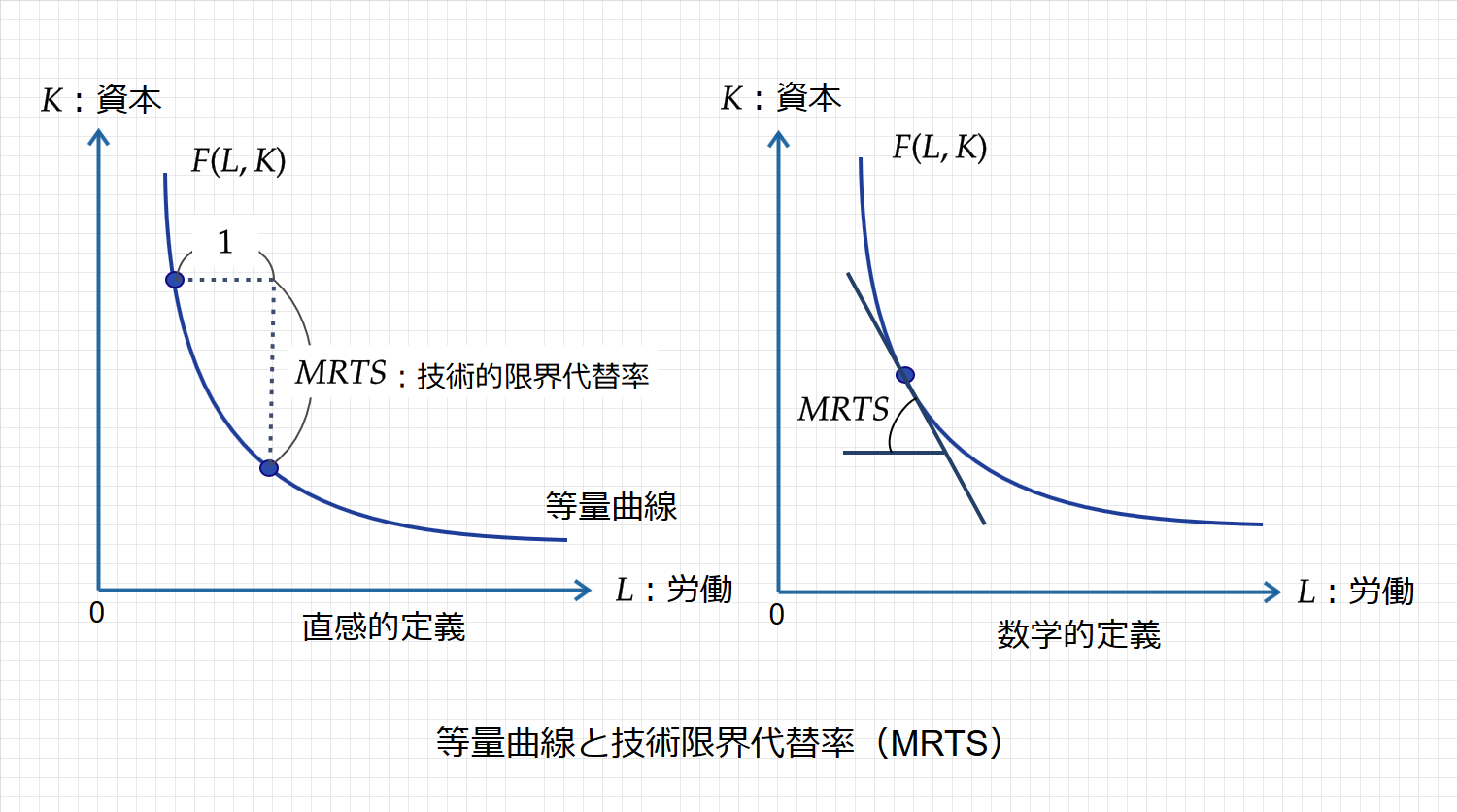
技術的限界代替率(MRTS)は、次のように図示できます。
直感的定義:労働量( $\small L$ )を1単位増やしたときの資本量($\small K$)の減少分
数学的定義:等量曲線の接線の傾き
ここでは、労働と資本の代替関係を表しています。
解釈は無差別曲線の限界代替率と同じなので、合わせて覚えてしまいましょう。
【総費用関数】等費用曲線と費用最小化【MRTS】

費用最小化条件を押さえる。
総費用関数と等費用曲線の導出
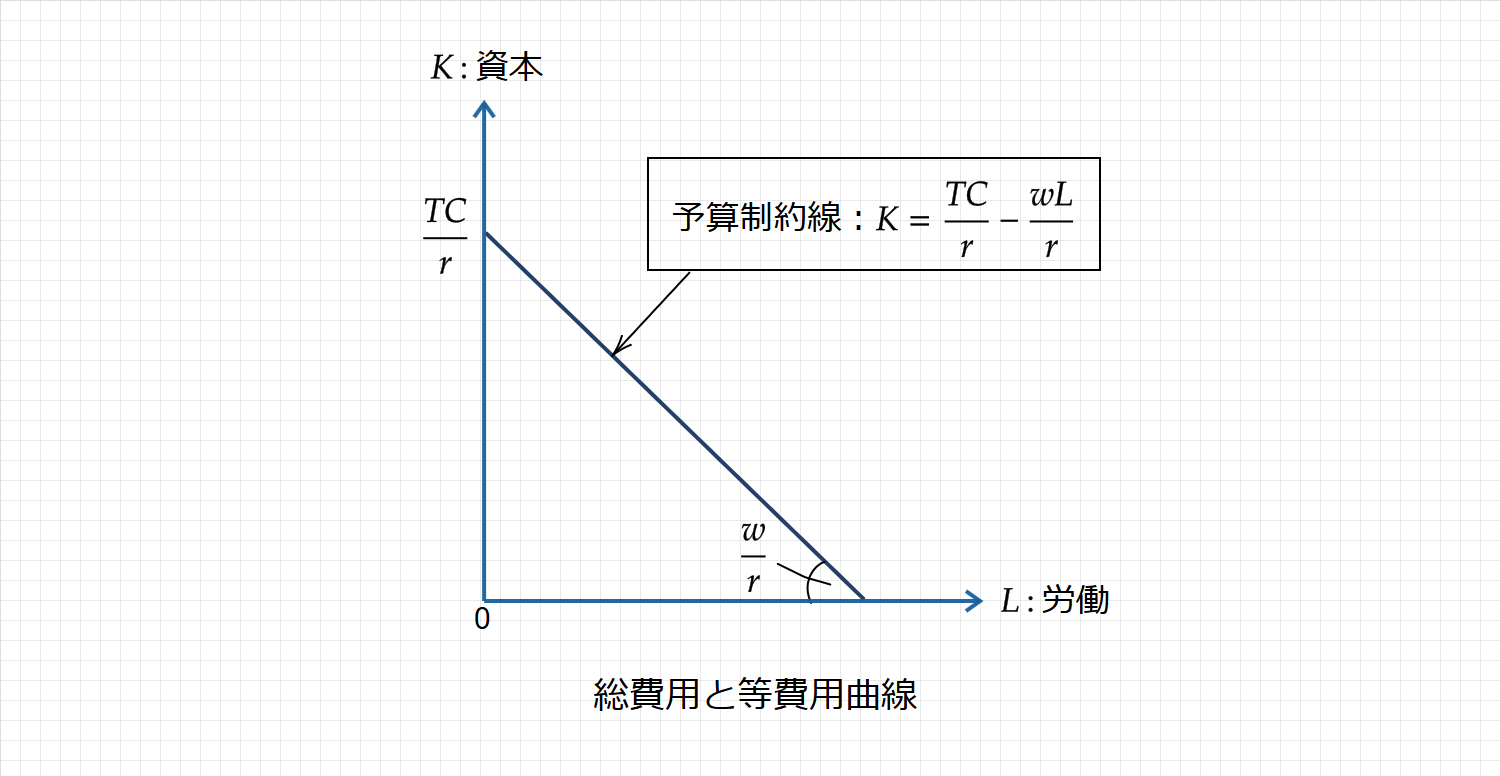
等費用曲線は、総費用関数(TC)から導出され、次のように図示できます。
$\small TC=wL+rK$$\\$$\small K=\displaystyle \frac{TC}{r}-\displaystyle \frac{wL}{r}$$\\$($\small TC$:総費用、$\small L$:労働、$\small K$:資本、$\small w$:賃金率、$\small r$:資本レンタル率)
$\small w$:労働に対する賃金
$\small r$:資本レンタル率
⇒資本を調達するためのコスト(例:生産のためにトラックを借りたときなど)
これは企業の予算制約線と言われ、切片は$\small \displaystyle \frac{TC}{r}$、傾きの大きさは$\small \displaystyle \frac{w}{r}$で表されます。
この総費用曲線と等量曲線を組み合わせて、費用最小化条件について考えます。
技術的限界代替率と費用最小化条件(MRTS)
等費用曲線と等量曲線を使うと、費用最小化条件は次のように図示されます。
$\\$$\small MRTS=\frac{\displaystyle MP_L}{\displaystyle MP_K}=\displaystyle \frac{w}{r}$$\\$($\small MP_L$:労働の限界生産力、$\small MP_K$:資本の限界生産力、$\small w$:賃金率、$\small r$:資本レンタル率)
―費用最小化問題―
$\\$$\small min\,\,K=\displaystyle \frac{TC}{r}-\displaystyle \frac{wL}{r}$$\\$$\small s.t. \,\,F(L,K)$
「生産関数の下で、総費用を最小化する」
⇒ $\small min$ は「minimize:最小化する」を、$\small s.t.$ は「subject to:条件の下で」の意。
等量曲線上では、生産量が一定となるため、企業の予算制約線を動かし、総費用が最小化される点$\small E^*(L,K)$で労働($\small L$)と資本($\small K$)が決定されます。
以上、消費者理論の場合、予算を使い切るという発想ですが、生産者理論では企業の生産量は一定として、最小限の労働と資本を決める発想のため、この費用は最小化されます。
おわりに:等量曲線と等費用曲線、技術的限界代替率の関係を理解する
等量曲線と等費用曲線の関係は、消費者理論の効用最大化と逆の考え方⇔費用最小化です。
技術的限界代替率は「限界代替率」の考え方と一緒なので、理解をすり合わせていきましょう。

以上となります。参考になった方は応援もよろしくお願いします!
【参考文献】
尾山・安田(2013)『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏(2014)『ミクロ経済学の力』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】





コメント