こんにちは、とし(@tyobory)です。
ミクロ経済学第10回テーマは「MC曲線・AC曲線・AVC曲線」です。
第9回では、企業利潤の最大化と最適生産についてまとめました。まだ未学習の方は、下記の記事をご参考ください。

全体の目次:「MC曲線・AC曲線・AVC曲線」
2.$\small AC$曲線:平均費用曲線
3.$\small AVC$曲線:平均可変費用曲線
本記事では、総費用に関連して、MC曲線・AC曲線・AVC曲線について掘り下げ、それぞれの関連性について考察していきます。
【ミクロ経済学】MC曲線・AC曲線・AVC曲線【3つの費用曲線を理解する】

費用概念を曲線する。
3種類の費用【限界費用・平均費用・平均可変費用】
これまで企業の利潤を算出するにあたり、総費用($\small TC$)を取り扱ってきました。ここで、損益分析するために、下記の3種類の費用概念を導入して考えていきます。
- 限界費用($\small MC$:$\small Marginal \, Cost$)
- 平均費用($\small AC$:$\small Average \, Cost$)
- 平均可変費用($\small AVC$:$\small Average \, Variable \,Cost$)
限界費用($\small MC:\small \frac{\partial TC }{\partial Q})$):生産量を1単位増加させたときの総費用の増加分
平均費用($\small AC:\frac{TC }{Q})$):生産量Qのときの1単位当たりの費用
平均可変費用($\small AVC:\frac{VC }{Q}$):生産量Qのときの固定費を除いた1単位当たりの費用
この3つの費用をマスターすることにより、企業利益の損益分岐点と、企業がこれ以上、生産を行うべきかどうかの操業停止点を把握できるようになります。
以下、各費用概念を取り上げ、グラフと数式で確認していきます。
MC曲線【限界費用曲線】
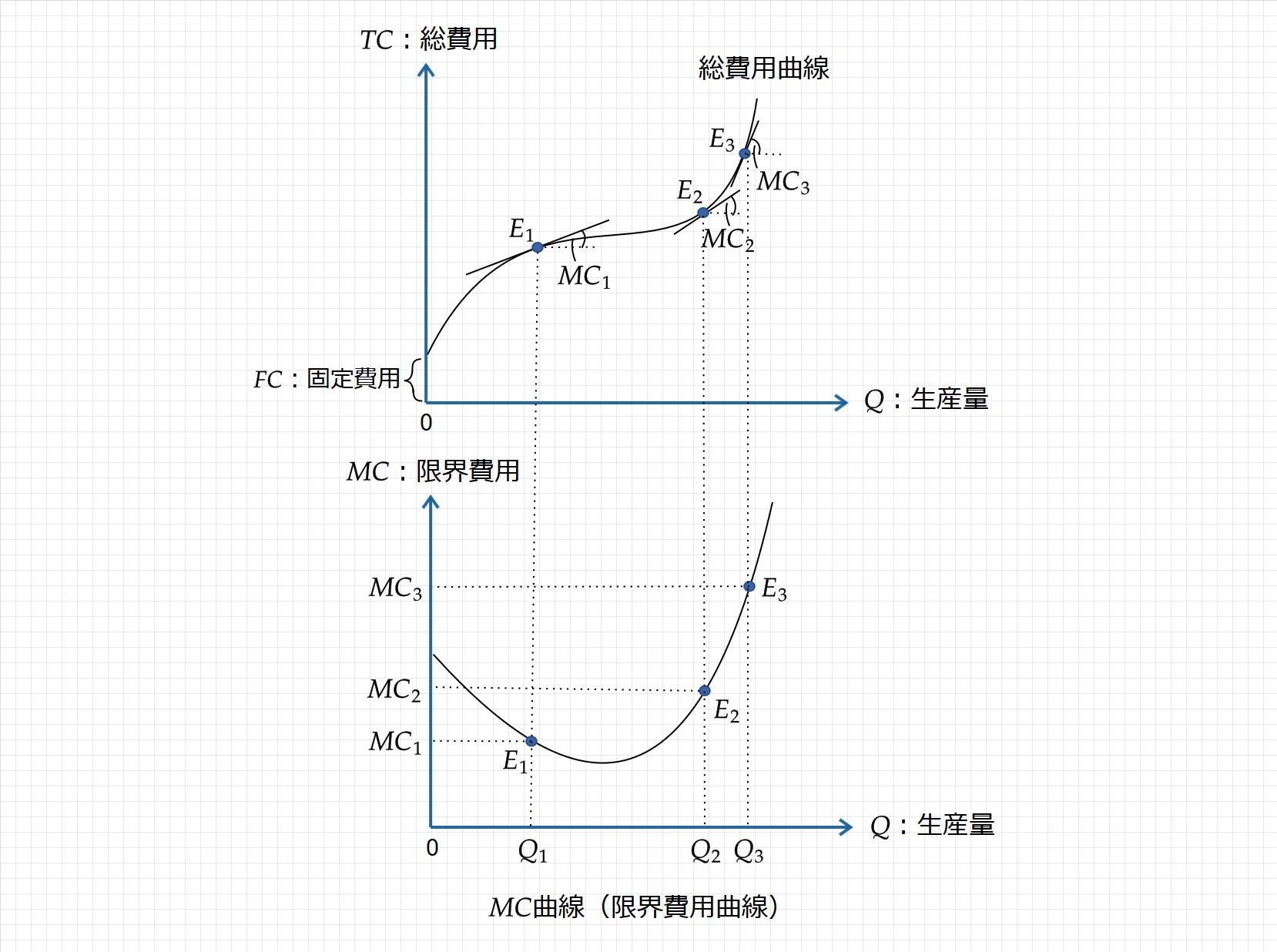
限界費用($\small MC$)は、総費用曲線の接線の傾きで表され、次のように図示されます。
限界費用($\small MC$)とは、生産量を1単位増加させたときの総費用の増加分であり、総費用曲線の接線の傾きで表されます。下図は、限界費用の軌跡を図示したものである。
当初、生産量が増加すると、協力効果により限界費用は逓減し、接線の傾きが小さくなるため、$\small MC$曲線は右下がりとなります。そして、$\small Q_1$と$\small Q_2$の間で最低点を通り、ある地点から混雑効果により限界費用は逓増し、$\small MC$曲線は接線の傾きを大きくし、右上がりの曲線となります。
以上をまとめると、初め限界費用は減少していき、$\small Q_1$と$\small Q_2$の間で最少となり、ある地点から限界費用は上昇し続けることになります。
AC曲線【平均費用曲線】
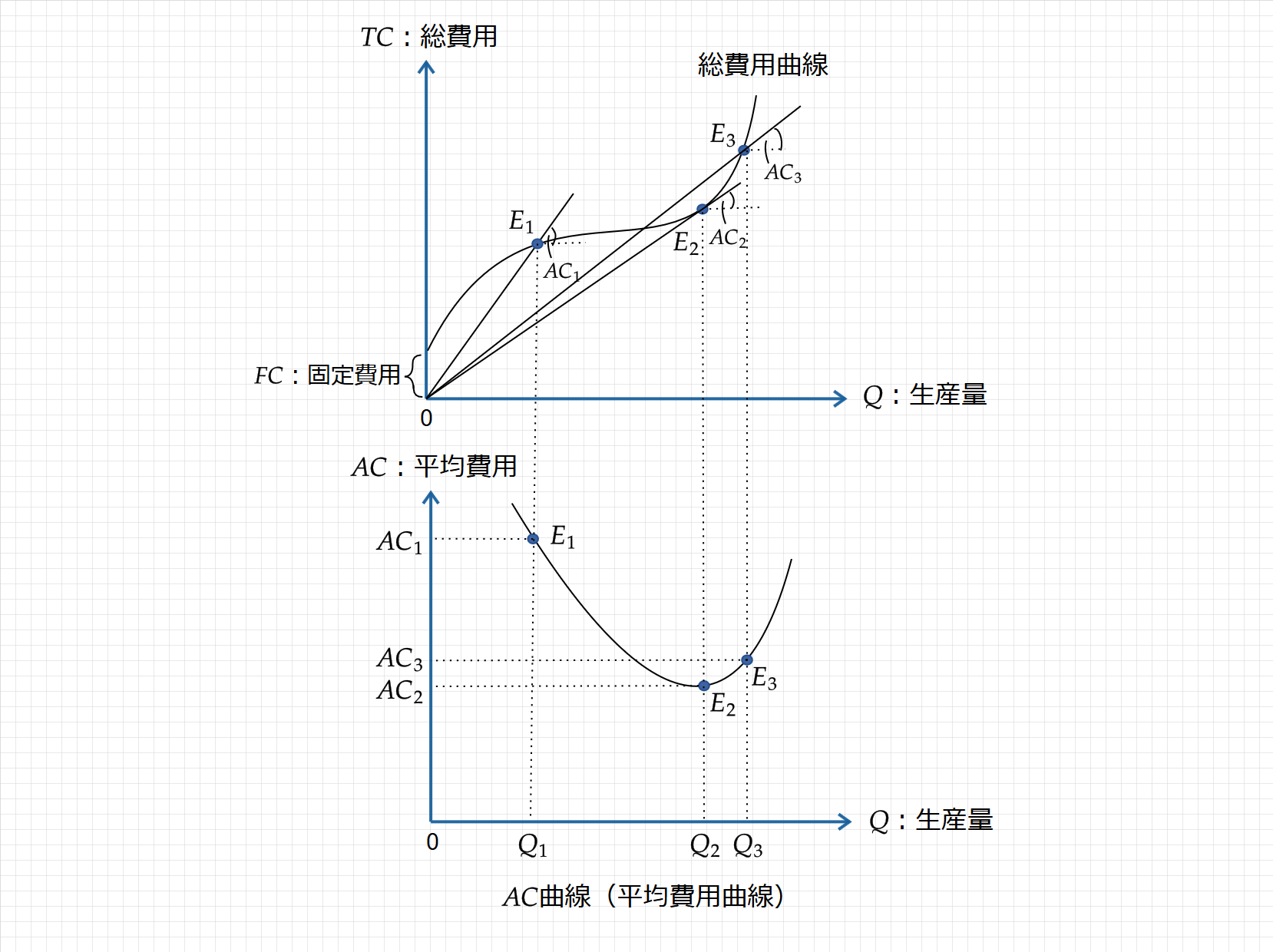
$\small AC$曲線(平均費用曲線)は、原点Oと総費用曲線上の点を結ぶ直線の傾きで表され、次のように図示されます。
生産量が増加すると、製品1個当たりの費用は徐々に下がっていくため、当初AC曲線は右下がりとなります。そして、TC曲線とAC曲線が接するE点で、平均費用(AC)は最小値をとり、再びAC曲線は上昇に転じます。
TC曲線とAC曲線が接する点で、ACは最小となる($\small E_2$点)
このように、AC曲線の最小値は、MC曲線の最小値と異なり、総費用曲線と接する点であることを理解しましょう。
AVC【平均可変費用曲線】
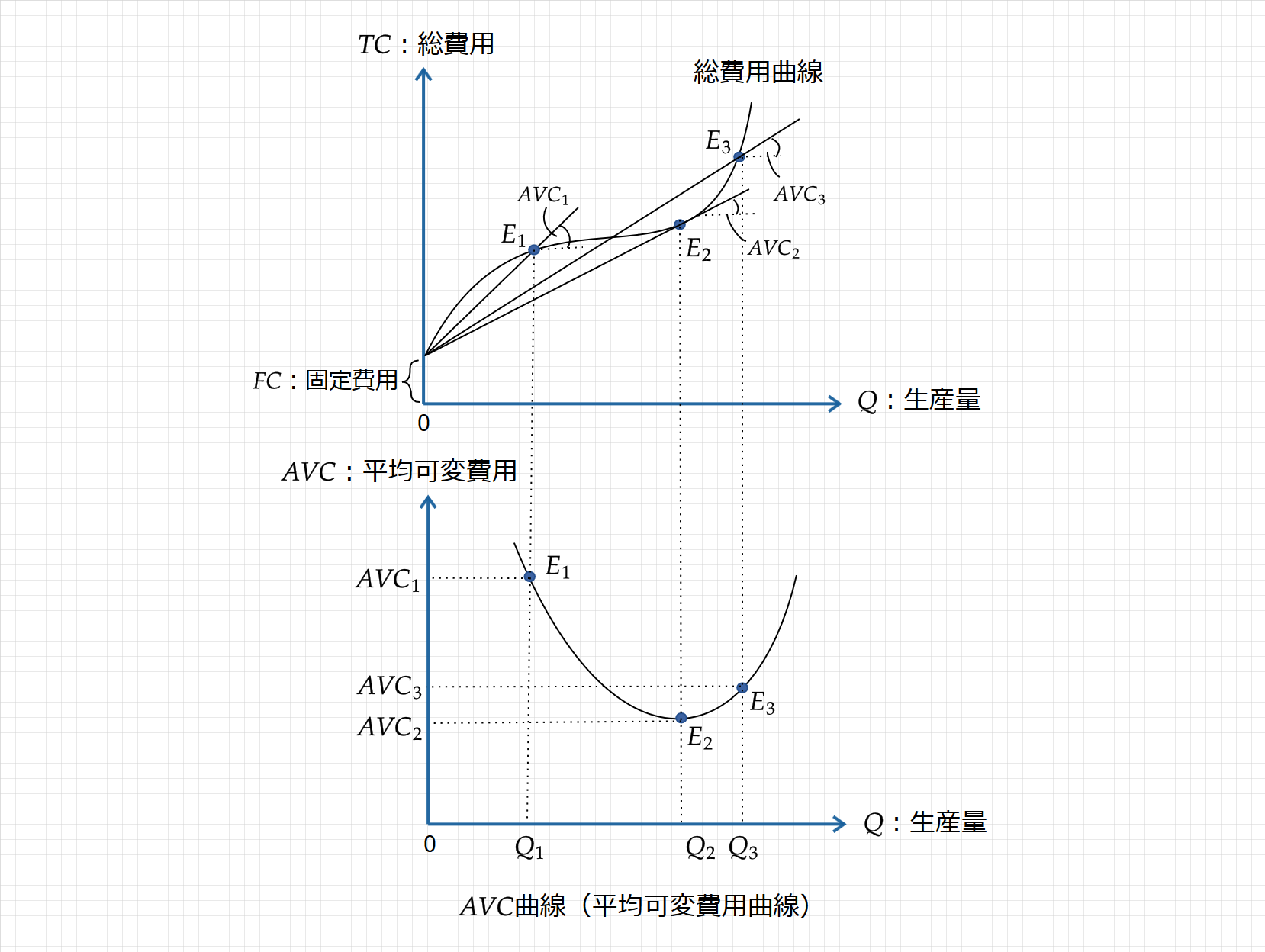
$\small AVC$曲線(平均可変費用曲線)は、可変費用曲線の出発点と総費用曲線上の点を結ぶ直線の傾きで表され、次のように図示されます。
$\small AVC$曲線(平均可変費用曲線)は、固定費用($\small FC$)を含まない分、AC曲線よりも下側に位置します。
AC(平均費用)と同様に、TC曲線とAVC曲線が接する点で、AVCは最小となる($\small E_2$点)
このように、MC曲線・AC曲線・AVC曲線が導出され、図示されます。次に、損益分岐点と操業停止点について掘り下げていきます。
MC曲線・AC曲線・AVC曲線の関係性【損益分岐点と操業停止点】

企業はどこまで生産を続ける?
MC曲線・AC曲線・AVC曲線の関係【損益分岐点と操業停止点】
MC曲線・AC曲線・AVC曲線をすべて足し合わせて図示すると、次のようになります。
ここで最も大切なことは、MC曲線がAC曲線とAVC曲線の最低点を通ることです。
MC曲線(限界費用曲線)はTC曲線(総費用曲線)の接線の傾きの大きさで示され、AC曲線とAVC曲線の傾きが最小となる点で、MC曲線の傾きと等しくなります(したがって最低点を通る)。
そして、企業の利潤と生産活動を分析すると…
MC曲線とAC曲線の交点が損益分岐点であり、MC曲線とAVC曲線の交点が操業停止点として示されます。
損益分岐点と操業停止点(グラフで解説)
MC曲線・AC曲線・AVC曲線より、企業の供給曲線を図示することができます(下図、赤線)。
まず、損益分岐点($\small E_p$)より市場価格が高いとき(P>AC)、企業の利益は黒字となります。逆に、損益分岐点($\small E_p$)より市場価格が低いとき(P<AC)、企業の利益は赤字となります。
ここで、企業は利益が赤字になったとしても、生産を止めることはしません。なぜなら、固定費用の一部を回収できている状態にあるからです。
企業が本当に生産を止めるのは、操業停止点よりも市場価格が低くなったときです(P<AVC)。このとき、固定費用の一部すら回収できなくなるため、企業は操業を停止します。
補論:損益分岐点と操業停止点(数式で解説)
最後に、なぜ損益分岐点がP=ACで、操業停止点がP=AVCになるのかを数式で確認します。
まず、企業の利潤関数は次のように表されます。
$\small \Pi =TR-TC$
$\small \Pi =PQ-(VC+FC)$
この生産量$\small Q$でまとめ方により、色々見えてきます。ここで、総費用(TC)全体を生産量$\small Q$でまとめてみましょう。
$\small \Pi =Q(P-\frac{\displaystyle (VC+FC)}{\displaystyle Q})$
$\small \Pi =Q(P-AC)$
このように、総費用(TC)を生産量(Q)で割ると平均費用(AC)が導かれます。つまり。企業はP>ACのときに黒字となり、P<ACのときに赤字となるわけです。
他方で、総費用のうち可変費用(VC)だけ生産量$\small Q$で括ることにしましょう。すると、
$\small \Pi =Q(P-\frac{\displaystyle (VC)}{\displaystyle Q})-FC$
$\small \Pi =Q(P-AVC)-FC$
式からも明らかなように、市場価格(P)が平均可変費用(AVC)よりも高いとき、固定費用は赤字だが、可変費用の部分は回収できています。
つまり、P>AVCのときは「固定費用の一部を回収できている状態」にあり、企業は価格(P)が平均可変費用(AVC)を下回らない限り生産を続けることになります。
おわりに:MC曲線・AC曲線・AVC曲線の関係性を理解する
基本的には、MC曲線・AC曲線・AVC曲線をグラフで書けるようになれば、損益分岐点も操業停止点もすんなりと理解できるようになります。
もちろん、費用関数がS型ではなく、直線の場合もあるので、問題文などに応じてグラフを書いて考えていきましょう。以下、復習です。
・MC曲線は、AC曲線とAVC曲線の最低点を通る
・損益分岐点:P=MC=AC
・操業停止点:P=MC=AVC

以上となります。参考になった方は応援もよろしくお願いします!
【参考文献】
尾山・安田(2013)『経済学で出る数学: 高校数学からきちんと攻める』日本評論社.
神取道宏(2014)『ミクロ経済学の力』日本評論社.
マクロ経済学の学習はこちら マクロ経済学を学ぶ【記事一覧】
ミクロ経済学の学習はこちら ミクロ経済学を学ぶ【記事一覧】
編入希望の方はこちら 【編入】独学で経済学部の編入試験に合格する方法【ロードマップ】





コメント